SURFACE AREA AND VOLUME OF 3D SHAPES

CUBE

In Geometry, a Cube is a solid three-dimensional figure, which has 6 square faces, 8 vertices and 12 edges.

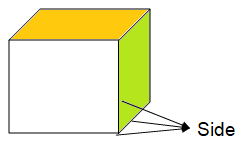
Volume of cube = a³

Lateral surface area = 4a²

Total surface area = 6a²

To find side length of cube from the diagonal, we use the formula

Side length = a√3

RECTANGULAR PRISM

In geometry, a rectangular prism can be defined as a 3-dimensional solid shape which has six faces that are rectangles. A rectangular prism is also a cuboid.

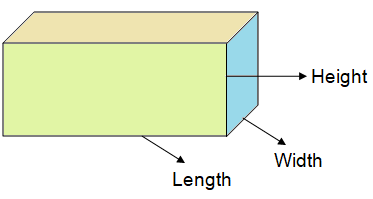
Lateral surface area = 2h(l + w)

Total surface area = 2(lw + wh + hl)

Volume = length x width x height

TRINAGULAR PRISM

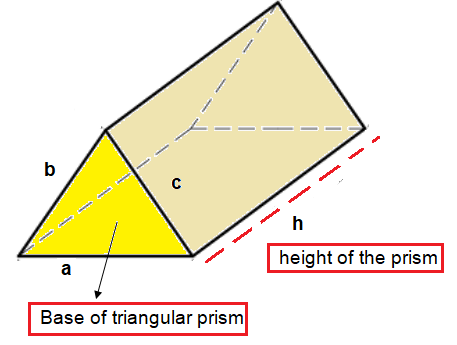
Lateral surface area = ph

p = Perimeter of the triangle and h = height of the prism

Total surface area = ph + 2B

B = Base area of triangular prism

Volume = Base area x height

CYLINDER

A cylinder is a three dimensional solid that holds two parallel bases joined by a curved surface at a fixed distance.

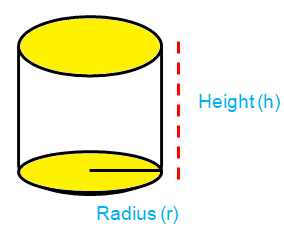
Lateral surface area of cylinder = 2πrh

Total surface area = 2πr(h + r)

Volume of cylinder = πr²h

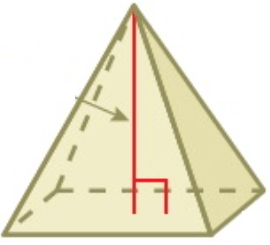
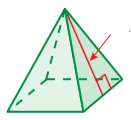
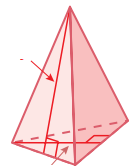
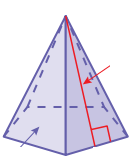
PYRAMID

A pyramid is a 3D polyhedron with the base of a polygon along with three or more triangle-shaped faces that meet at a point above the base

Surface area of pyramid = Area of all faces

Volume = (1/3) x base area x height

SPHERE

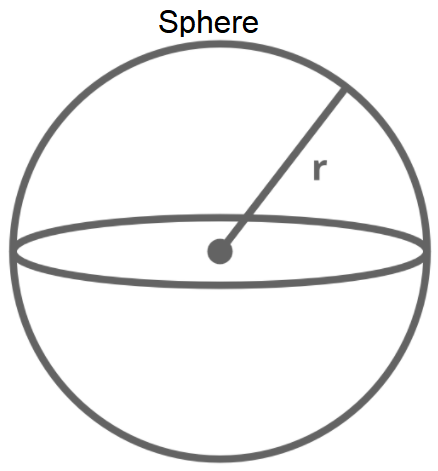
Formula for surface area of a sphere,

S = 4πr²

Formula for volume of a sphere 

V = (4/3)πr³

(where r is the radius of the sphere)

CONE

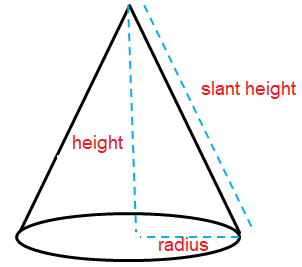
Formula for surface area of a cone,

Lateral surface area  = πrl

Total surface area = πr(l + r)

Formula for volume of a cone

V = (1/3)πrl