VOLUME OF SQUARE PYRAMID
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
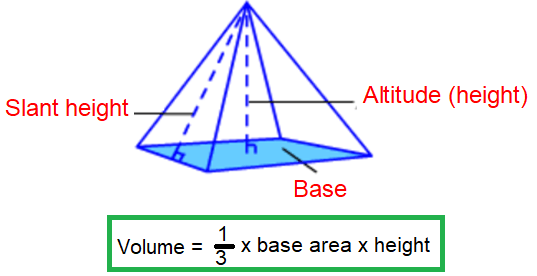
To calculate volume
- Find the base area
- Multiply it by height
- Multiply this by 1/3
For the answer use cubic units.
Find the volume of the square pyramids given below.
Problem 1 :
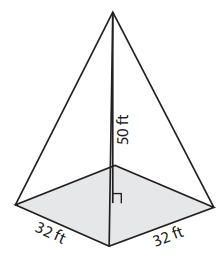
Solution :
Base is in the shape of square
Base area = area of square
Area of square = (Side)2
= (32)2
Height = 50 ft
Volume of pyramid = (1/3) x (32)2 x 50
= 17066.6 ft3
Problem 2 :
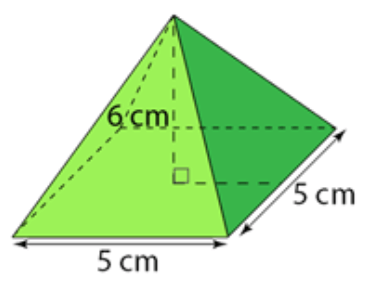
Solution :
Base area = area of square
height = 6 cm
Area of square = 52
Volume = (1/3) x 52 x 6
= 50 cm3
Problem 3 :
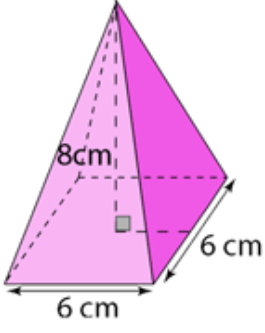
Solution :
Base area = area of square
height = 8 cm
Area of square = 62
Volume = (1/3) x 62 x 8
= 96 cm3
Problem 4 :
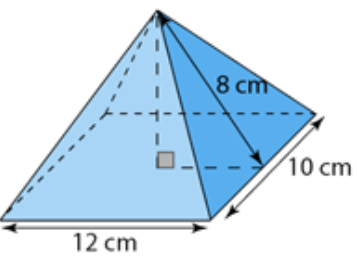
Solution :
Base area = area of square
Let height = h cm
Slant height = 8 cm
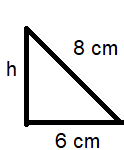 |
Using Pythagorean theorem h2 + 62 = 82 h2 + 36 = 64 h2 = 64 - 36 h2 = 28 h = 5.29 |
Area of square = 122
= 144
Volume = (1/3) x 144 x 5.29
= 253.92 cm3
Problem 4 :
Find the volume of the square pyramid with a height of 15 in and a slant height of 17 in. The square base measures 16 by 16 inches.
Solution :
Base length of square = 16 inches
height = 15 in
slant height = 17 in
Volume of square pyramid = (1/3) x 162 x 15
= 1280 cubic inches
Problem 5 :
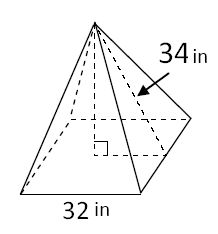
Solution :
Base length = 32 in
Slant height = 34 in
height = h
h2 + 162 = 342
h2 + 256 = 1156
h2 = 1156 - 256
h2 = 900
h = 30
Volume = (1/3) x 322 x 30
= 1024 x 10
= 10240 cubic inches
Problem 6 :
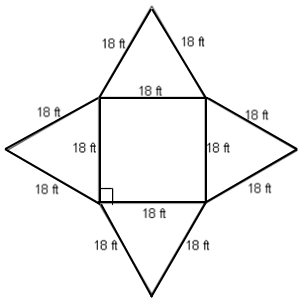
Solution :
When we fold this shape, we will get square base pyramid.
Volume of the square pyramid = (1/3) x base area x height
Base area = 182
= 324 square feet
Considering the equilateral triangle.
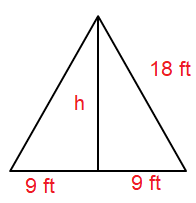
h2 + 92 = 182
h2 + 81 = 324
h2 = 324 - 81
h2 = 243
h = 15.58
Volume = (1/3) x 324 x 15.58
= 108 x 15.58
= 1682.64 cubic ft
Problem 7 :
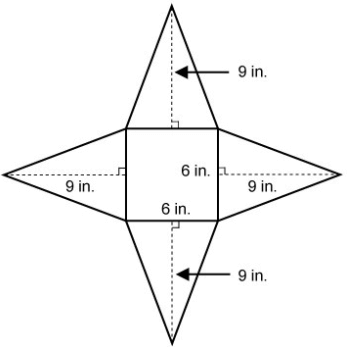
Solution :
Area of the base = 62 ==> 36
height = 9 in
Volume = (1/3) x 36 x 9
= 108 cubic inches
Problem 8 :
Originally, Khafre’s Pyramid had a height of about 144 meters and a volume of about 2,218,800 cubic meters. Find the side length of the square base.

Solution :
Volume of pyramid = 2,218,800 cubic meters
Height = 144 m
(1/3) x base area x height = 2,218,800
Let x be the side length of base of square.
(1/3) ⋅ x2 ⋅ 144 = 2,218,800
x2 = 2,218,800 (3) / 144
x2 = 46225
x = √46225
x = 215 meter
Problem 9 :
A pyramid with a square base has a volume of 128 cubic inches and a height of 6 inches. Find the side length of the square base.
Solution :
(1/3) x base area x height = 128 cubic inches
Let x be the side length of base of square.
Height = 6 inches
(1/3) ⋅ x2 ⋅ 6 = 128
x2 = (128/6)(3)
x2 = 64
x = √64
x = 8 inches
Problem 10 :
A pyramid with a rectangular base has a volume of 6 cubic feet. The length of the rectangular base is 3 feet and the width of the base is 1.5 feet. Find the height of the pyramid.
Solution :
(1/3) x base area x height = 128 cubic inches
Let x be the side height of hte pyramid.
Length = 3 ft, width = 1.5 ft and height = x
(1/3) ⋅ 3 ⋅ 1.5 ⋅ x = 128
x = [ 128/(3 ⋅ 1.5) ] ⋅ 3
x = 85.33 feet
Problem 11 :
A pyramid with a triangular base has a volume of 18 cubic centimeters. The height of the pyramid is 9 centimeters and the height of the triangular base is 3 centimeters. Find the width of the base.
Solution :
Volume of the triangular base = 18 cubic centimeter
Height of the pyramid = 9 cm
height of triangular base = 3 cm
(1/3) x base area x height = 18
1/3 x 1/2 x base x height x height of prism = 18
1/6 x base x 3 x 9 = 18
base = (18 x 6)/(3 x 9)
= 4 cm
So, the measure of width of the base is 4 cm.
Problem 12 :
The pyramids are similar. Find the volume of pyramid B.
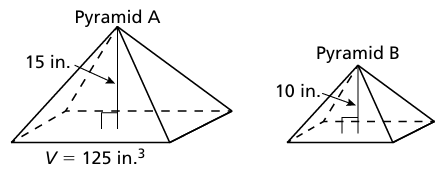
Solution :
Since the two shapes are similar, their corresponding sides will be in the same ratio. The ratio of cubes of corresponding sides will be equal to the ratio of cubes of volume of these figures.
(15/10)3 = Volume of pyramid A/Volume of pyramid B
(15/10)3 = 125/Volume of pyramid B
125/1000 = 125/Volume of pyramid B
Volume of pyramid B = 125/0.125
= 1000 in3
So, volume of pyramid B is 1000 in3.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling