Making Math Meaningful

The ultimate aim of our website is to give valuable math content for students, teachers, educational institutions and all math lovers. We always aim to make the students to understand the concept in depth with our content. We give concept, examples, solved problems, practice questions, quiz and worksheet for each stuff in math. 

We order the stuff in each concept of math as follows : 

1. Lower order thinking

2. Middle order thinking

3. Higher Order thinking

When students start learning algebra in math, first they learn variables and constants. Without understanding variables and constants, it is impossible to understand the other stuff in algebra. To understand variables, consider the height of a plant. Is the height of a plant is same everyday ? The answer is no. Because, the plant is growing everyday and the height will change. So, height of a plant is variable. To understand constants, consider $100 currency. Does $100 currency have different values in different states in America ? The answer is no. At everywhere of America, $100 currency will have the same value. So, the number 100 is a constant. 

Consider the following two simple problems in algebra :  

In the above two problems, we have the same alphabet x. Since we have the same alphabet x, do we get the same value for x in both the problems ? No. We get different values for x. If you consider some other problems with the alphabet x, you may get a different value. Even though we have the same alphabet x, we don't get the same value for it. That is, the value of x changes. So, x is a variable. When we have alphabets x, y and z in algebra, usually we consider them as variables. Sometimes, we consider some alphabets as constants as a special case. 

In geometry, consider the term 'measure of arc'. Is it the length of arc ? No. Measure of arc is the angle made at the center of the circle by that arc. central angle of the arc. 

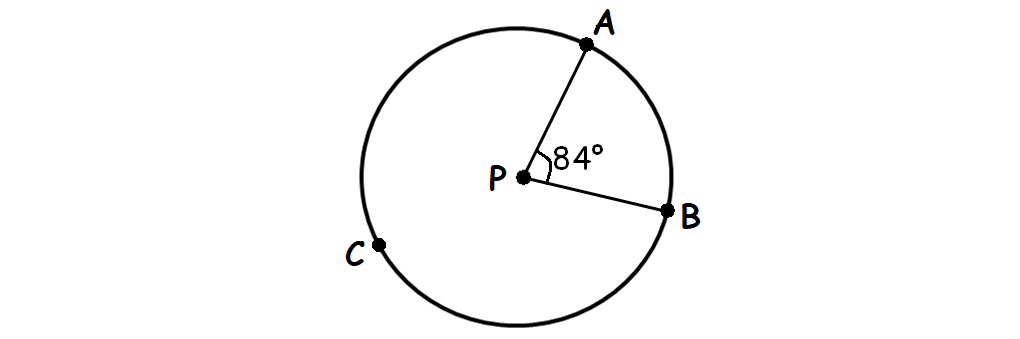
In the diagram above, the measure of arc AB is 84°. Length of arc is the distance from A to B on the circle. 

Many students always try to memorize the formula for finding length of arc, that is 

Length of arc = (θ/360°) x 2πr

Length of arc is a fractional part of circumference of the circle. To get the length of an arc, we need to find what fraction of the circumference is equal to length of the arc and the fraction is given by θ/360°, where θ is the central angle of arc. So, we multiply the fraction θ/360° by the circumference of the circle to get the length of arc. 

Similarly, area of sector is a fractional part of area of the circle.  To get area of a sector, we need to find what fraction of area of the circle is equal to area of sector and the fraction is given by θ/360°, where θ is the central angle of arc. So, we multiply the fraction θ/360° by the area of circle. 

Area of sector = (θ/360°) x πr²

In this way, if you understand the concept, you don't have to memorize the formulas.  

We are planning to cover all the areas of math soon. You can browse more math content in our website. 

Thanks.