TRANSFORMATIONS OF 2D SHAPES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
There are three kinds of isometric transformations of 2D shapes.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Translation of 2D Shapes
A translation is transformation in which every point of figure moves a fixed distance in a given direction.
- Number of units of horizontal movements can be considered as "x".
- Number of units of vertical movements can be considered as "y".
- Translation vector will be in the form (x, y)
- If x is positive, then we have to move x units to the right→
- If x is negative, then we have to move x units to the left ←.
- If y is positive, then we have to move y units up ↑ .
- If y is negative, then we have to move y units down ↓.
Related Pages
Rotation of 2D Shapes
Rotating the shape means moving them around a fixed point. There are two directions
i) Clockwise
ii) Counter clockwise (or) Anti clockwise
The shape itself stays exactly the same, but its position in the space will change.
|
90° clockwise 90° counter clockwise 180° 270° clockwise 270° counter clockwise |
(x, y) ==> (y, -x) (x, y) ==> (-y, x) (x, y) ==> (-x, -y) (x, y) ==> (-y, x) (x, y) ==> (y, -x) |
Related Pages
- Rotation of 2D shapes
- Rotation in coordinate plane
- 90 degree rotation on a coordinate plane
- 90 degree rotation of 2D shapes worksheet
- Rules for 90 degree and 270 degree rotation
- 270 degree rotation on 2D shapes
- 90 degree rotation on a coordinate plane worksheet
- 270 degree rotation of 2D shapes worksheet
- Rotation of 2D shapes with given center of rotation
- Rotation of 2D shapes with center of rotation
- Rotation of 2D shapes practice problems
Reflection of 2D Shapes
The reflected image will be congruent to the original.
What is line of reflection ?
A reflection maps every point of a figure to an image across a fixed line. The fixed line is called the line of reflection.
Reflections can be performed easily in the coordinate plane using the general rules below.
Types of reflectionsReflection over x axis Reflection over y axis Reflection over y = x Reflection over y = -x Reflection about origin |
Rules(x, y) ==> (x, -y) (x, y) ==> (-x, y) (x, y) ==> (y, x) (x, y) ==> (-y, -x) (x, y) ==> (-x, -y). |
Related Pages
- Examples on reflection across x-axis
- Problems on reflection across x-axis
- Worksheet on reflection across x-axis
- Examples on reflection across y-axis
- Problems on reflection over y-axis
- Worksheet on reflection over y-axis
- Example problems on reflection across y = x
- Problems on reflection of y = x
- Worksheet of reflection on y = x and -x
- Example problems on reflection across y = -x
- Problems on y = -x
- Worksheet of reflection on y = x and -x
- Reflection across horizontal line
- Reflection across vertical line
- Write a rule to describe the reflection
- From the given points find the rule of reflection
- Reflection in coordinate plane
- Reflection on coordinate plane worksheet
The object A has been translated to give an image B in each diagram. Give the translation in each case.
Problem 1 :
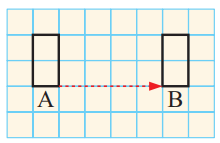
Solution :
Observing the vertex of A to vertex of rectangle B, only horizontal movement is done.
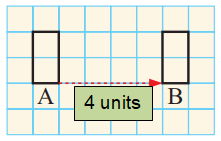
Moved 4 units right, so the required translation vector is (4, 0).
Problem 2 :
Translate the shape 2 units right and 1 unit up.
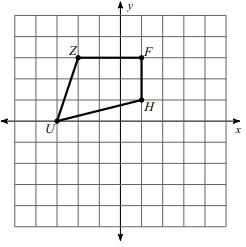
Solution :
Writing the vertices,
U (-3, 0), Z (-2, 3), F (1, 3) and H (1, 1)
We translate the figure 2 units right and 1 unit up. So,
(x, y) ===> (x + 2, y + 1)
U (-3, 0) ==> U' (-3+2, 0+1) ==> U' (-1, 1)
Z (-2, 3) ==> Z' (-2+2, 3+1) ==> Z' (0, 4)
F (1, 3) ==> Z' (1+2, 3+1) ==> F' (3, 4)
H (1, 1) ==> H' (1+2, 1+1) ==> Z' (3, 2)
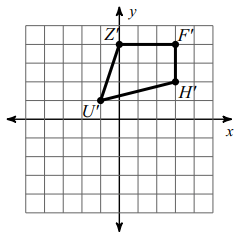
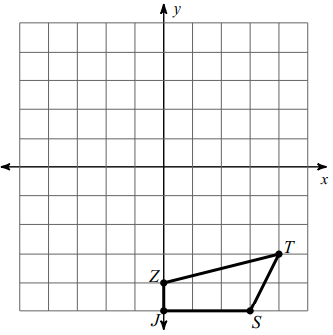
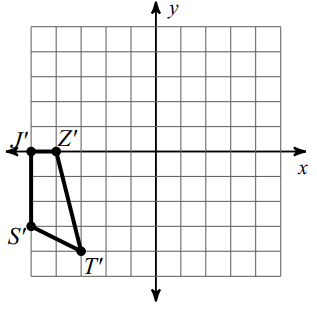
Problem 3 :
Rotation 90° clockwise about the origin.
Solution :
Marking the coordinate,
Z (0, -4), J (0, -5), T (4, -3) and S (3, -5)
Rotation ==> 90° clockwise
Rule :
(x, y) ==> (y, -x)
Z (0, -4) ==> Z' (-4, 0)
J (0, -5) ==> J' (-5, 0)
T (4, -3) ==> T' (-3, -4)
S (3, -5) ==> S'(-5, -3)
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling