90 DEGREE ROTATION ON A COORDINATE PLANE

Graph the image of the figure using the transformation given.

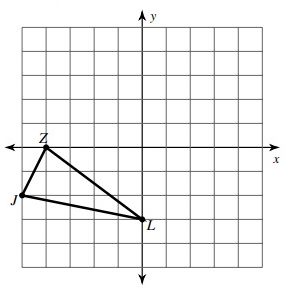
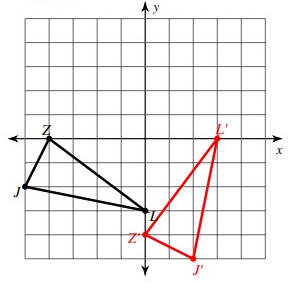
Problem 1 :

rotation 90° counterclockwise about the origin.

Solution:

Given, J = (-5, -2), Z = (-4, 0) and L = (0, -3)

Here, triangle is rotated 90° counterclockwise. So, the rule that we have to apply here is

(x, y) ---> (-y, x)

J(-5, -2) = J'(2, -5)

Z(-4, 0) = Z'(0, -4)

L(0, -3) = L'(3, 0)

Vertices of the rotated figure are 

J'(2, -5), Z'(0, -4) and L'(3, 0)

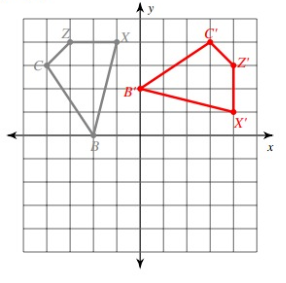
Problem 2 :

rotation 90° clockwise about the origin

B(-2, 0), C(-4, 3), Z(-3, 4), X(-1, 4)

Solution:

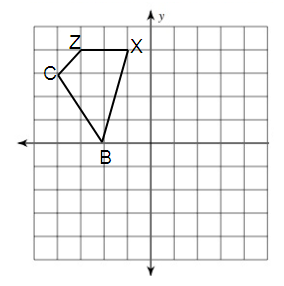
Here, triangle is rotated 90° counterclockwise. So, the rule that we have to apply here is

(x, y) ---> (-y, x)

B(-2, 0) = B'(0, -2)

C(-4, 3) = C'(-3, -4)

Z(-3, 4) = Z'(-4, -3)

X(-1, 4) = X'(-4, -1) 

Vertices of the rotated figure are 

B'(0, -2), C'(-3, -4), Z = (-4, -3) and X'(-4, -1)

Rotate the figure as indicated. Label the image using prime notation.

Problem 3 :

rotation 90° counterclockwise about the origin.

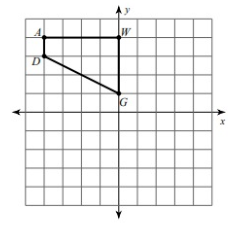
Solution:

Given, A = (-4, 4), D = (-4, 3), G = (0, 1) and W = (0, 4)

Here, triangle is rotated 90° counterclockwise. So, the rule that we have to apply here is

(x, y) ---> (-y, x)

A(-4, 4) = A'(-4, -4)

D(-4, 3) = C'(-3, -4)

G(0, 1) = G'(-1, 0)

W(0, 4) = W'(-4, 0)

Vertices of the rotated figure are 

A'(-4, -4), D'(-3, -4), G'(-1, 0) and W'(-4, 0)

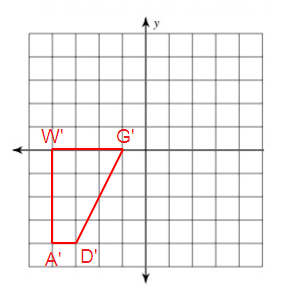
Problem 4 :

rotation 90° counterclockwise about the origin

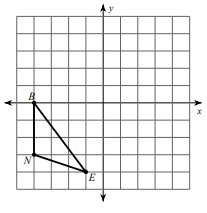
Solution:

Given, B = (-4, 0), N = (-4, -3) and E = (-1, -4)

Here, triangle is rotated 90° counterclockwise. So, the rule that we have to apply here is

(x, y) ---> (-y, x)

B(-4, 0) = B'(0, -4)

N(-4, -3) = N'(3, -4)

E(-1, -4) = E'(4, -1)

Vertices of the rotated figure are 

B'(0, -4), N'(3, -4) and E'(4, -1)

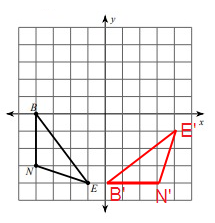
Problem 5 :

rotation 90° counterclockwise about the origin

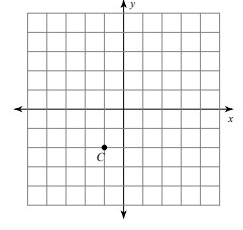
Solution:

Given, C = (-1, -2)

Here, triangle is rotated 90° counterclockwise. So, the rule that we have to apply here is

(x, y) ---> (-y, x)

C(-1, -2) = C'(2, -1)

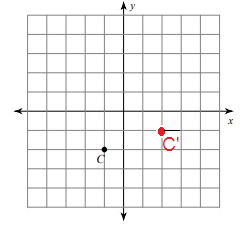
Problem 6 :

rotation 90° counterclockwise about the origin

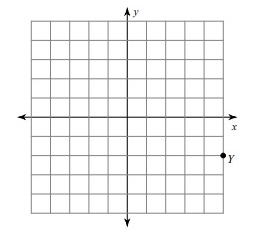
Solution:

Given, Y = (5, -2)

Here, triangle is rotated 90° counterclockwise. So, the rule that we have to apply here is

(x, y) ---> (-y, x)

Y(5, -2) = Y'(2, 5)

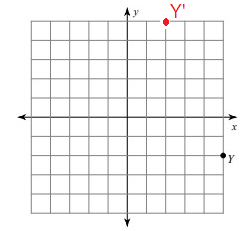
Problem 7 :

rotation 90° counterclockwise about the origin

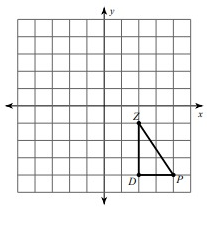
Solution:

Given, Z = (2, -1), D = (2, -4) and P = (4, -4)

Here, triangle is rotated 90° counterclockwise. So, the rule that we have to apply here is

(x, y) ---> (-y, x)

Z(2, -1) = Z'(1, 2)

D(2, -4) = D'(4, 2)

P(4, -4) = P'(4, 4)

Vertices of the rotated figure are 

Z'(1, 2), D'(4, 2) and P'(4, 4)

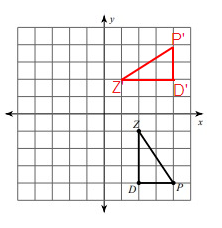
Problem 8 :

rotation 90° counterclockwise about the origin

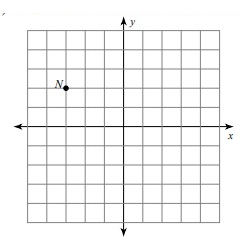
Solution:

Given, N = (-3, 2)

Here, triangle is rotated 90° counterclockwise. So, the rule that we have to apply here is

(x, y) ---> (-y, x)

N(-3, 2) = N'(-2, -3)

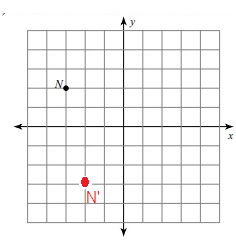
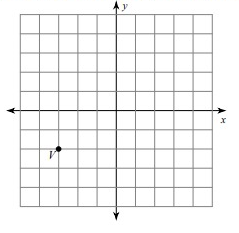
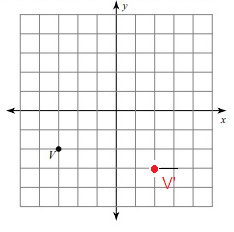
Problem 9 :

rotation 90° counterclockwise about the origin

Solution:

Given, V = (-3, -2)

Here, triangle is rotated 90° counterclockwise. So, the rule that we have to apply here is

(x, y) ---> (-y, x)

V(-3, -2) = V'(2, -3)