THEOREMS ON CIRCLES

Angles Subtended at the Arc

Theorem :

When two angles subtended by the same arc, the angle at the center of the circle is twice the angle at the circumference.

Proof :

Considering the circle with center O, now placing the points A, B and C on the circumference.

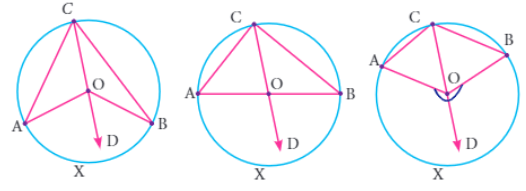
∠ACO = ∠OAC

∠BCO = ∠OBC

∠AOD = Exterior angle of the triangle

∠AOD = ∠ACO + ∠OAC  ----(1)

∠BOD = ∠BCO + ∠OBC  ----(2)

(1) + (2)

∠AOD + ∠BOD = (∠ACO + ∠OAC) + (∠BCO + ∠OBC)

∠AOB = (∠ACO + ∠OAC) + (∠BCO + ∠OBC)

∠AOB = 2∠OCA + 2∠OCB

∠AOB = 2(∠OCA + ∠OCB)

∠AOB = 2∠ACB

Related Pages

• Angle subtended at the center of the arc
• Worksheet on angle subtended at the center of the arc

Angles on the Same Segment

Angles subtended by the same arc at the circumference are equal. This means that angles in the same segment are equal

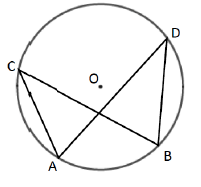
∠ACB = ∠ADB

Related Pages

• Examples on angles in the same segment of circle
• Angles in same segment of circle worksheet

Line Drawn from the Center to Tangent

A tangent is a straight line that touches the circumference of a circle at only one point. The angle between a tangent and the radius is 90˚.

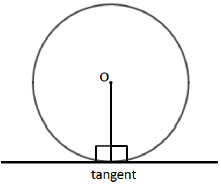
• The line which is drawn from the center of the circle to tangent of that circle is simply known as the radius of that circle.
• The radius will be perpendicular on the tangent in this case.
• The radius is the half of the diameter of the same circle.

Related Pages

• Line drawn from the center to the tangent
• Examples on line drawn from the center to tangent
• Line from the center to tangent of the circle worksheet

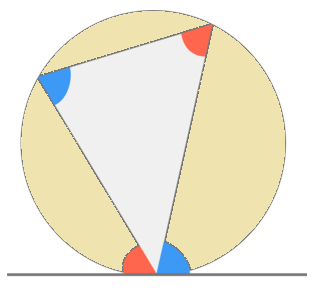
Alternate Segment Theorem

In any circle, the angle between a chord and a tangent through one of the end points of the chord is equal to the angle in the alternate segment.

Related Pages

• Examples on alternate segment theorem
• Worksheet on alternate segment theorem

Angle in Semicircle

The angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.

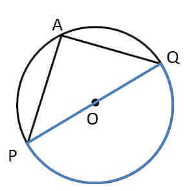
∠POQ = 180

2∠PAQ = ∠POQ

2∠PAQ = 180

∠PAQ = 180/2

∠PAQ = 90

Related Pages

• Example problems on angle in semicircle
• Angles in semicircle worksheet

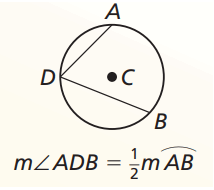
Inscribed Angle Intercepted Arc of the Circle

What is inscribed angle ?

Angle whose vertex is on the circle ang whose sides are chords of a circle.

Intercepted arc ?

The arc that lies between two chords on the inscribed angle.

Measure of an inscribed angle is half of its intercepted arc.

Related Pages

• Examples on inscribed angle and intercepted arc
• Inscribed angles and intercepted arc worksheet

Cyclic Quadrilateral and Intercepted Arc

A cyclic quadrilateral is a quadrilateral which has all its four vertices lying on a circle. It is also sometimes called inscribed quadrilateral.

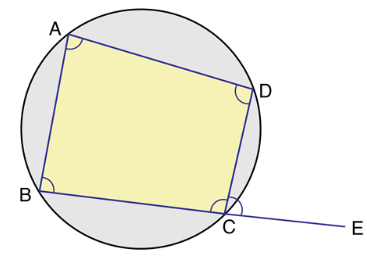
In which opposite angles are supplementary.

Exterior angle is equal to opposite interior angle. That is, in the above cyclic quadrilateral

∠DCE = ∠BAD

Related Pages

• Find missing angles in cyclic quadrilateral
• Cyclic quadrilateral and intercepted arc worksheet
• Problems on cyclic quadrilateral and intercepted arc

Intersecting Chords

If two chords intersect inside a circle, then the measure of each angle formed is one half the sum of the measures of the arcs intercepted by the angle and its vertical angle.

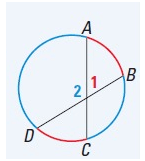
m∠1 = 1/2(mCD + mAB),

m∠2 = 1/2(mAD + mBC)

Related Pages

• Properties of angles formed by intersecting chords
• Problems on intersecting chords inside the circle
• Angle formed by two chords intersecting chords inside the circle

Intersecting Secants Theorem

The measure of an angle formed by two secants, a secant and a tangent, or two tangents intersecting in the exterior of a circle is equal to one-half the positive difference of the measures of the intercepted arcs.

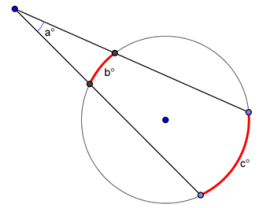
Related Pages

• Intersecting secant theorem
• Intersecting secants theorem worksheet

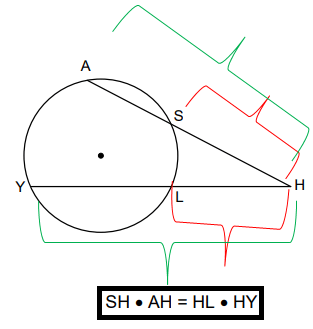
Secants Intersecting Outside of Circle

AH and HY are the two secant segments intersecting at point H. SH is the external secant segment of the whole secant segment AH, and LH is the external secant segment of HY. Thus, according to the theorem, we have

SH × AH = HL × HY

Related Pages

• Finding lengths of secants in the exterior of circle
• Finding length of secants intersecting lines outside circle worksheet

Chord Chord Product Theorem

The products of the lengths of the line segments on each chord are equal.

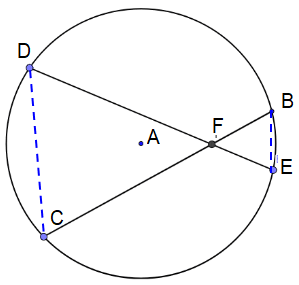
CF ⋅ BF = DF ⋅ EF

Related Pages

• Chord chord product theorem
• Chord chord product theorem worksheet

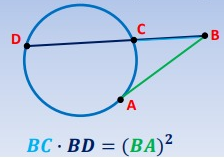
Secant Tangent Product Theorem

If a secant and tangent share a point then the product of the secant and external part is equal to tangent squared.

• Secant tangent product theorem
• Secant tangent product theorem worksheet