FINDING LENGTHS OF TWO SECANTS INTERSECTING IN THE EXTERIOR OF CIRCLE

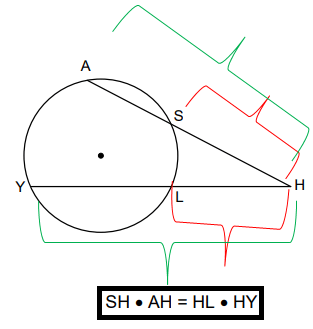
AH and HY are the two secant segments intersecting at point H. SH is the external secant segment of the whole secant segment AH, and LH is the external secant segment of HY. Thus, according to the theorem, we have

SH × AH = HL × HY

Find the value of x in the following.

Problem 1 :

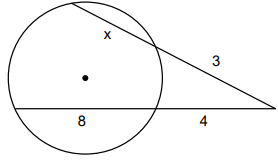
Solution :

3 • (x + 3) = 4 • (8 + 4)

3(x + 3) = 4 (12)

x + 3 = 16

x = 16 - 3

x = 13

Problem 2 :

CD and EF are chords of the circle with centre O. The chords meet at the point P, which is outside of the circle

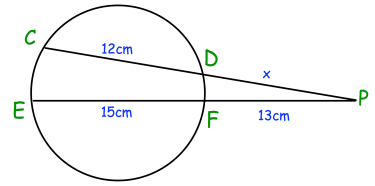
Solution :

PD • PC = PF • PE

x • (x + 12) = 13 • (13 + 15)

x(x + 12) = (13 • 28)

x² + 12x = 364

x² + 12x - 364 = 0

(x + 26)(x - 14) = 0

x = -26 and x = 14

Problem 3 :

CD and EF are chords of the circle below. The chords meet at the point P, which is outside of the circle.

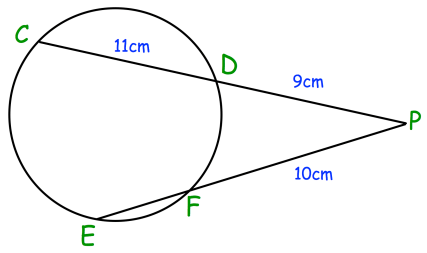
Solution :

PD • PC = PF • PE

9 • (9 + 11) = 10 • (10 + EF)

Let EF be x.

9 • (20) = 10 • (10 + x)

10 + x = 180/10

10 + x = 18

x = 18 - 10

x = 8

Problem 4 :

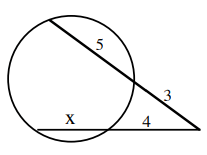
Solution :

3 • (3 + 5) = 4 • (4 + x)

3 • 8 = 4 • (4 + x)

Dividing by 4 on both sides.

6 = 4 + x

x = 6 - 4

x = 2

Problem 5 :

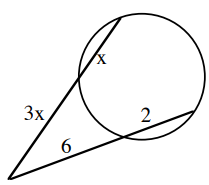
Solution :

x • (x + 3x) = 2 • (2 + 6)

x • 4x = 2 • 8

4x² = 16

Dividing by 4 on both sides.

x² = 4

x = 2

Problem 6 :

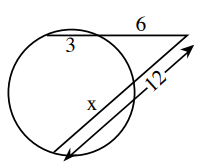
Solution :

6 • (6 + 3) = (12 - x) • 12

6(9) = 12(12 - x)

54 = 12(12 - x)

Dividing by 12 on both sides,

4.5 = 12 - x

x = 12 - 4.5

x = 7.5

Problem 7 :

CD and EF are chords of the circle with centre O. The chords meet at the point P, which is outside of the circle.  Calculate the area of triangle OEF.

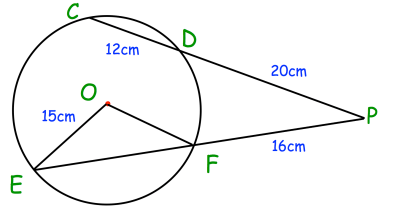
Solution :

OE = OF (radii)

PD • PC = PF • PE

20 • (20 + 12) = 16 • (16 + EF)

20 (32) = 16 (16 + EF)

Dividing by 16 on both sides.

20(2) = 16 + EF

EF = 40 - 16

EF = 24

Drawing the perpendicular from O.

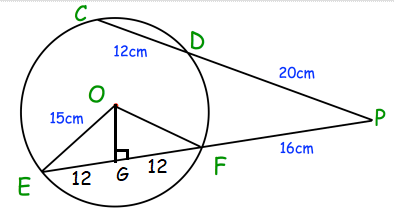
In triangle OGF,

OF² = OG² + GF²

15² = OG² + 12²

225 - 144 = OG²

OG² = 81

OG = 9

Area of triangle OEF = (1/2) x base x height

= (1/2) x 24 x 9

= 12 x 9

= 108 cm²