EXPONENTIAL FUNCTION CONTEXT AND DATA MODELING

Below is the table of values for exponential function is in the form

f(x) = a (b)^x + k

Write the equation that represents each table.

Problem 1 :

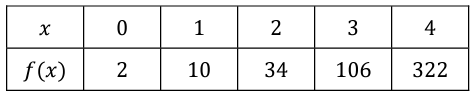
Solution :

f(x) = a (b)^x + k

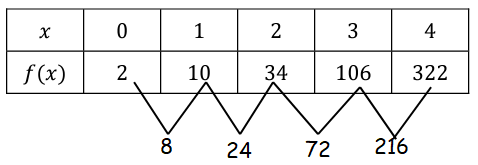
Multiplication factor = 3 = b

f(x) = a (3)^x + k

When x = 0 and f(0) = 2

2 =  a (3)⁰ + k

2 = a(1) + k

2 = a + k

k = 2 - a

When x = 1 and f(1) = 10

10 =  a (3)¹ + k

10 = a(3) + k

10 = 3a + k

10 = 3a + 2 - a

10 - 2 = 2a 

2a = 8

a = 4

When a = 4, k = 2 - 4 ==> -2

Applying the value of a and k, we get

f(x) = 4 (3)^x - 2

Problem 2 :

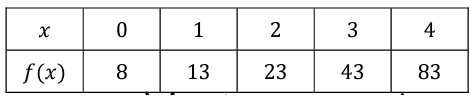
Solution :

f(x) = a (b)^x + k

Multiplication factor = 2 = b

f(x) = a (2)^x + k

When x = 0 and f(0) = 8

8 =  a (2)⁰ + k

8 = a(1) + k

8 = a + k

k = 8 - a

When x = 1 and f(1) = 13

13 =  a (2)¹ + k

13 = a(2) + k

13 = 2a + k

13 = 2a + 8 - a

13 - 8 = a

5 = a

When a = 5, k = 8 - 5 ==> 3

Applying the value of a and k, we get

f(x) = 5 (2)^x + 3

Problem 3 :

Solution :

f(x) = a (b)^x + k

Multiplication factor = 5 = b

f(x) = a (5)^x + k

When x = 0 and f(0) = 5

5 =  a (5)⁰ + k

5 = a(1) + k

5 = a + k

k = 5 - a

When x = 1 and f(1) = 29

29 =  a (5)¹ + k

29 = 5a + k

29 = 5a + k

29 = 5a + 5 - a

29 - 5 = 4a

24 = 4a

a = 6

When a = 6, k = 5 - 6 ==> -1

Applying the value of a and k, we get

f(x) = 6 (5)^x - 1

Problem 4 :

Mr. Sullivan left out his Pico-Chile-Mucho-Caliente salsa, and it is starting to grow mold. The table below gives the area of the mold, in square centimeters, at time 𝑡 days

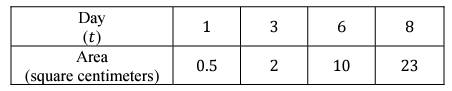
a. Use an exponential regression 𝐴(𝑡) = 𝑎𝑏^t to model these data. Round to three decimals but store the original equation in your calculator.

b. According to the model in your calculator, how large will the surface of the mold be after 7 days?

c. According to the model in your calculator, how large will the surface of the mold be after 10 days?

d. When will the area of the mold reach 34 cm²?

Solution :

Applying the point (1, 0.5), we get

0.5 = ab¹

ab = 0.5 ------(1)

Applying the point (3, 2), we get

2 = ab³

ab³ = 2 ------(2)

Applying the point (6, 10), we get

10 = ab⁶

ab⁶ = 10 ------(3)

Applying the point (8, 23), we get

23 = ab⁸

ab⁸ = 23 ------(4)

(4) / (3)

ab⁸ / ab⁶ = 23/10

b² = 2.3

b = 1.517

b = (2 + 1.710 + 1.517)/3

= 1.742

Applying the value of b in (1), we get

ab = 0.5

a(1.742) = 0.5

a = 0.5/1.742

a = 0.287

A(t) = 0.287 (1.742)^t

b. When t = 7

A(7) = 0.288 (1.741)⁷

= 0.288 (48.48)

= 13.97

c. When t = 10

A(10) = 0.288 (1.741)¹⁰

= 73.68

d. When A(t) = 34

34 = 0.288 (1.741)^x

34/0.288 = (1.741)^x

118.05 = (1.741)^x

log (118.05) = x log(1.741)

x = log(118.05)/log(1.741)

x = 2.072/0.241

x = 8.59

Approximately 8.59 days.