ANGLE IN SEMICIRCLE

The angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.

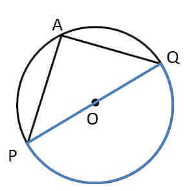
∠POQ = 180

2∠PAQ = ∠POQ

2∠PAQ = 180

∠PAQ = 180/2

∠PAQ = 90

Problem 1 :

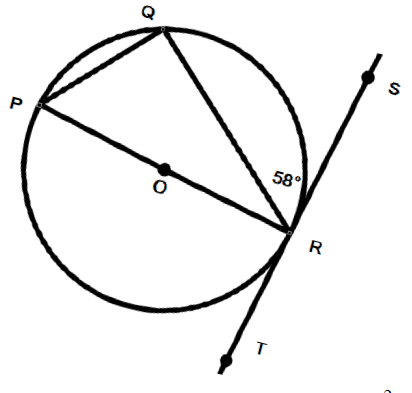
P, Q and R are points on the circumference of a circle, center O. PR is the diameter of the circle and ST is a tangent to the circle at the point R.

∠QRS = 58

a)  Work out the size of angle QRP.

b)  Work out the size of the angle QPR.

Solution :

∠ORS = 90

a)  Work out the size of angle QRP :

∠ORQ + ∠ORS = 90

∠ORQ + 58 = 90

∠ORQ = 90 - 58

∠ORQ = 32

∠QRP = 32

b)  Work out the size of the ∠QPR :

∠QPR = 180 - (∠QRP + ∠PQR)

∠QPR = 180 - (32 + 90)

∠QPR = 180 - 122

∠QPR = 58

Using alternate segment theorem, we can prove ∠QPR = 58.

Problem 2 :

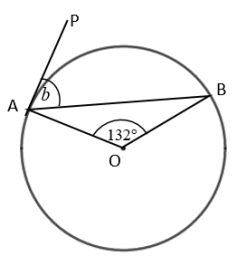
Work out the size of each angle marked with a letter. Give reasons for your answers.

Solution :

∠OAP = 90

∠OAB + ∠BAP = 90  ---(1)

In triangle OAB,

∠OBA + ∠OAB + ∠AOB = 180

Let ∠OBA = x

x + 132 + x = 180

2x + 132 = 180

2x = 180 - 132

2x = 48

x = 48/2

x = 24

By applying x = 24 in (1), we get

24 + ∠BAP = 90

∠BAP = 90 - 24

b = ∠BAP = 66

Problem 3 :

In the circle given below, U is the point of ST such that RUT is right angle.

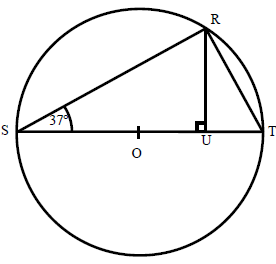
find 

a) ∠URT    b)  ∠ROT    c)  ∠ORU      d)  ∠ORT

Solution :

In the figure above,

∠SRT = 90 (angle in a semicircle)

In triangle RST,

∠RST + ∠SRT + ∠STR = 180

37 + 90 + ∠STR = 180

127 + ∠STR = 180

∠STR = 180 - 127

∠STR = 53

a) Finding ∠URT :

In triangle URT,

∠RUT + ∠TRU + ∠UTR = 180 

90 + ∠TRU + 53 = 180 

143 + ∠TRU = 180

∠TRU = 180 - 143

∠TRU = 37

b)  Finding ∠ROT :

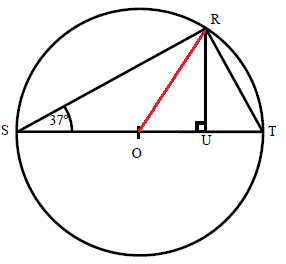
Since ∠OSR = ∠ORS = 37

∠ROT = 37 + 37 ==> 74

c)  Finding ∠ORU :

∠SRO + ∠ORU + ∠URT = 90

37 + ∠ORU + 37 = 90

74 + ∠ORU = 90

∠ORU = 90 - 74

∠ORU = 16

d)  Finding ∠ORT :

∠ORT = ∠ORU + ∠URT

∠ORT = 16 + 37

∠ORT = 53

Problem 4 :

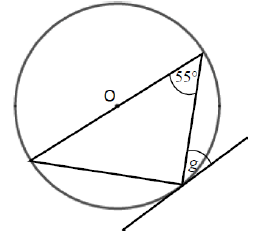
Solution :

In the triangle inside the circle, the angle in the semicircle is right angle.

55 + 90 + g(alternate segment) = 180

145 + g = 180

g = 180 - 145

g = 35

Problem 5 :

Work out the size of each angle marked with a letter. Give reasons for your answers.

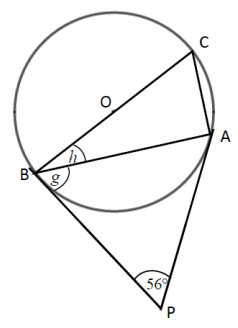
Solution :

∠PBA = ∠PAB = g

Because the tangent drawn from the external point of the circle will be equal in measure. So, its length will also will have same angle measure.

∠BPA + ∠PBA + ∠PAB = 180

56 + g + g = 180

56 + 2g = 180

2g = 180 - 56

2g = 124

g = 62

Since OB is the line drawn from center of the circle to the point of contact of the tangent.

g + h = 90

62 + h = 90

h = 90 - 62

h = 28

Problem 6 :

In the given figure O is the center of the circle and SP is a tangent. If ∠SRT = 65, find the values of x, y and and z.

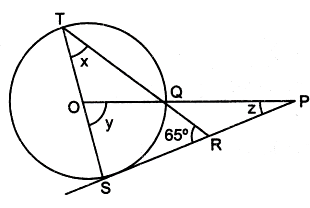
Solution :

In triangle STR,

∠SRT + ∠STR + ∠TSR = 180

65 + x + 90 = 180

x + 155 = 180

x = 180 - 155

x = 25

y = 2(25) ==> 50

In triangle SOP,

∠OSP + ∠SPO + ∠POS = 180

90 + z + y = 180

90 + z + 50 = 180

140 + z = 180

z = 180 - 140

z = 40

Problem 7 :

Work out the size of each angle marked with a letter. Give reasons for your answers.

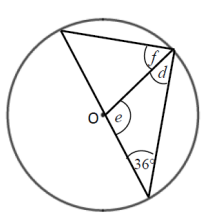
Solution :

From the picture, it is clear d = 36.

In the triangle,

e + d + 36 = 180

e + 36 + 36 = 180

e = 180 - 72

e = 108

f + d = 90

f + 36 = 90

f = 90 - 36

f = 54