PROBLEMS ON CYCLIC QUADRILATERAL AND INTERCEPTED ARC

Find the measure of angle and indicated arc.

Problem 1 :

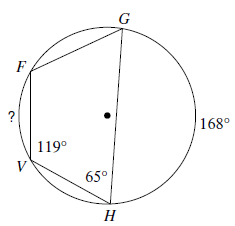
Solution :

In a cyclic quadrilateral, the opposite angles are supplementary.

∠FGH = 180 - 119 ==> 61

∠FGH = (1/2) Measure of arc (VH + FV)  ---(1)

∠GFV = 180 - 65 ==> 115

∠GFV = (1/2) Measure of arc (GH + VH) ---(2)

From (2)

115 = (1/2) (168 + measure of arc VH)

230 = 168 + measure of arc VH

Measure of arc VH = 230 - 168

Measure of arc VH = 62

By applying this value in (1)

61= (1/2) (62 + measure of arc FV) 

122 - 62 = measure of arc FV

Measure of arc FV = 60

Problem 2 :

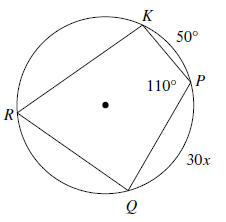
Solution :

In a cyclic quadrilateral, the opposite angles are supplementary.

∠KRQ = 180 - 110 ==> 70

∠KRQ = (1/2) (measure of arc PQ + KP)

70 = (1/2) (30x + 50)

140 = 30x + 50

140 - 50 = 30x 

30x = 90

x = 3

Problem 3 :

Find the values of x, y and z.

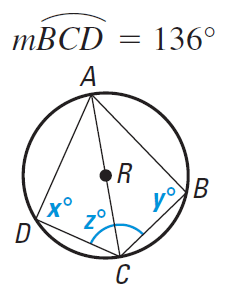
Solution :

∠DAB + ∠DCB = 180

∠DAB + z = 180 ---(1)

∠DAB = (1/2) measure of arc BD

∠DAB = (1/2) 136

∠DAB = 68

Applying the value of ∠DAB in (1), we get

z = 180 - 68

z = 112

∠ADC + ∠ABC = 180

x + y = 180

∠ADC = (1/2) Measure of arc AC

∠ADC = (1/2) 180

∠ADC = 90 = x

x = 90

Applying the value of x in x + y = 180, we get

90 + y = 180

y = 180 - 90

y = 90

Problem 4 :

Find the values of x, y and z.

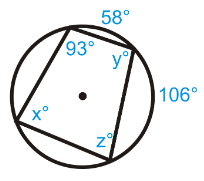
Solution :

x = (1/2) (106 + 58)

x = (1/2) (164)

x = 82

y = 180 - 82 (Opposite angles are supplementary)

y = 98

z = 180 - 93

z = 87

Problem 5 :

Find measure of angles A, B, C and D.

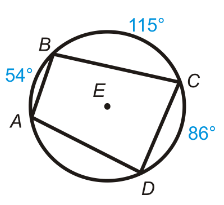
Solution :

∠BAD = (1/2) Measure of BD

∠BAD = (1/2) (115 + 86)

∠BAD = 100.5

∠BCD = 180 - 100.5

∠BCD = 79.5

∠ADC = (1/2)(54 + 115)

∠ADC = (1/2)(169)

∠ADC = 84.5

∠ABC = 180 - 84.5

∠ABC = 95.5

Problem 6 :

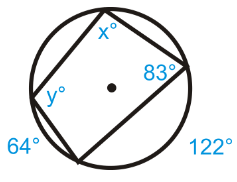
Solution :

x = (1/2)(64 + 122)

x = (1/2)(186)

x = 93

y = 180 - 83

y = 97

Problem 7 :

Find ∠DBC, ∠ACD

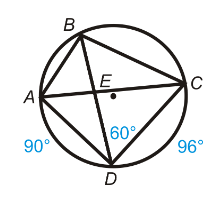
Solution :

∠DBC = (1/2)ABC Measure of arc DC

∠DBC = (1/2)96

∠DBC = 48

∠ACD = (1/2)ABC Measure of arc AD

∠ACD = (1/2)90

∠ACD = 45