PROBLEMS ON ALTERNATE SEGMENT THEOREM

In any circle, the angle between a chord and a tangent through one of the end points of the chord is equal to the angle in the alternate segment.

Problem 1 :

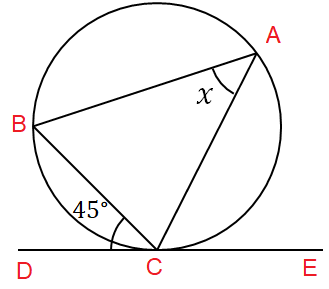
Find x.

Solution:

∠BCD = 45

BC, AB, AC are chords of the circle. DE is the tangent.

The angle between chord BC and tangent DE is 45 degree,

∠BCD = ∠BAC (alternate segments)

∠BAC = 45

Problem 2 :

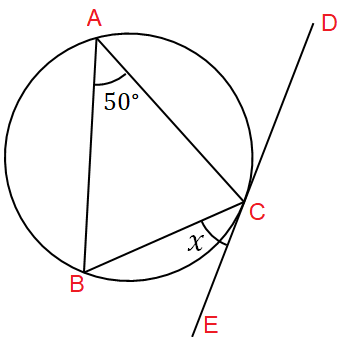
Find x.

Solution :

A and C are two endpoints of the chord AC.

Angle between the chord BC and the tangent DE = x

∠BCE = x

BC, AB, AC are chords of the circle. DE is the tangent.

The angle between chord BC and tangent DE is 45 degree,

∠BCE = ∠BAC (alternate segments)

∠BAC = 50

∠BCE = 50

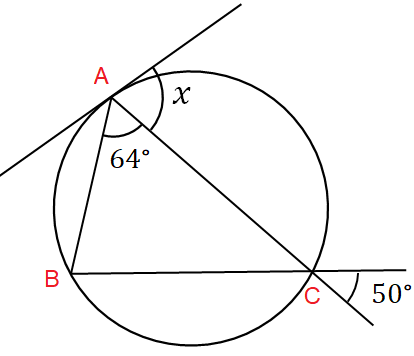
Problem 3 :

Solution :

∠BAC = 64, ∠BCA = 50 (vertically opposite angles)

In triangle ABC,

∠BAC + ∠BCA + ∠CBA = 180

64 + 50 + ∠CBA = 180

114 + ∠CBA = 180

∠CBA = 180 - 114

∠CBA = 66

Problem 4 :

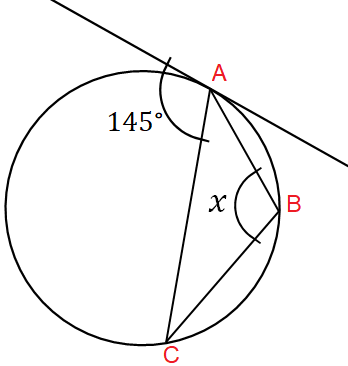
Solution :

∠ABC = x

AB is a chord, angle between one endpoint of the chord (A) and tangent is 145.

Alternate segment theorem ∠ABC = 145.

Problem 5 :

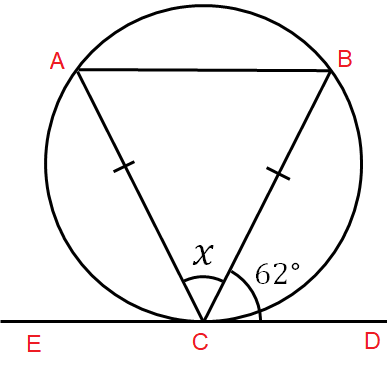
Solution :

∠CBA = 62 (Using alternate segment theorem)

∠BCD = 62

CB = AC = 62 (Sides of isosceles triangle)

In triangle ABC,

∠CAB + ∠ABC + ∠ACB = 180

62 + 62 + x = 180

124 + x = 180

x = 180 - 124

x = 56

Problem 6 :

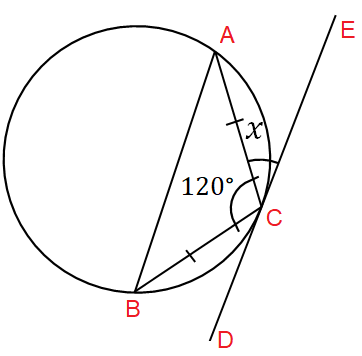
Solution :

In triangle ABC,

∠CBA + ∠ACB + ∠CAB = 180

Since it is isosceles triangle and CB = CA

∠CBA + 120 + ∠CBA = 180

2 ∠CBA = 180-120

∠CBA = 120/2

∠CBA = 60

∠CBA = x (Alternate segment)

x = 60

Problem 7 :

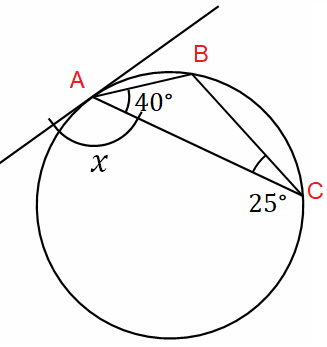
Solution :

In triangle ABC, sum of interior angles of a triangle.

∠ABC = 180 - (40 + 25)

∠ABC = 180 - 65

∠ABC = 115

x = 115 (Alternate segment)

Problem 8 :

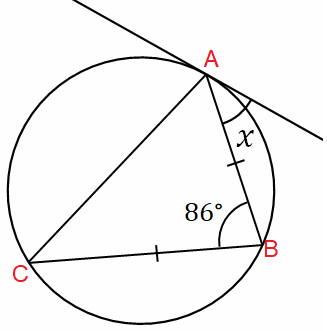
Solution :

BC = BA

In triangle ABC, sum of interior angles of a triangle.

∠ABC + ∠ACB + ∠BAC = 180

86 + ∠ACB + ∠ACB = 180

86 + 2∠ACB = 180

 2∠ACB = 180 - 86

 2∠ACB = 94

∠ACB = 94/2

∠ACB = 47

Problem 9 :

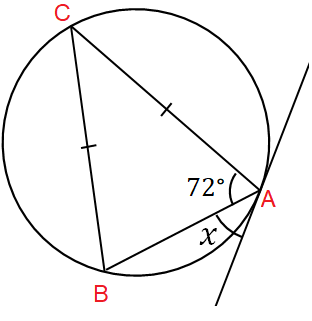
Solution :

CB = CA

In triangle ABC, sum of interior angles of a triangle.

∠ABC + ∠ACB + ∠BAC = 180

∠ABC + ∠ACB + 72 = 180

72 + 2∠ACB = 180

 2∠ACB = 180 - 72

 2∠ACB = 108

∠ACB = 108/2

∠ACB = 54