SECANT TANGENT PRODUCT THEOREM

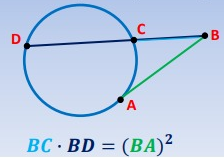
If a secant and tangent share a point then the product of the secant and external part is equal to tangent squared.

Problem 1 :

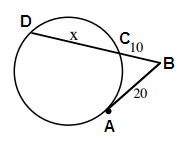
Solution:

BC ⋅ BD = (BA)²

10 ⋅ (10 + x) = (20)²

100 + 10x = 400

10x = 400 - 100

10x = 300

x = 30

Problem 2 :

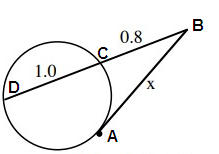
Solution:

BC ⋅ BD = (BA)²

0.8 ⋅ (0.8 + 1.0) = (x)²

0.8 (1.8) = x²

x² = 1.44

x = 1.2

Problem 3 :

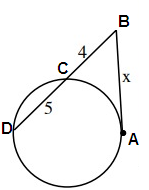
Solution:

BC ⋅ BD = (BA)²

4 ⋅ (4 + 5) = (x)²

4 (9) = x²

x² = 36

x = 6

Problem 4 :

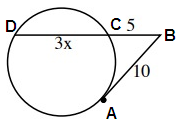
Solution:

BC ⋅ BD = (BA)²

5 ⋅ (5 + 3x) = (10)²

25 + 15x = 100

15x = 100 - 25

15x = 75

x = 75/15

x = 5

Problem 5 :

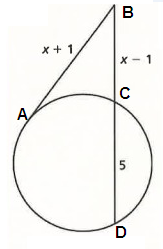
Solution:

BC ⋅ BD = (BA)²

(x - 1) ⋅ (x - 1 + 5) = (x + 1)²

(x - 1) ⋅ (x + 4) = (x² + 1 + 2x)

x² + 4x - x - 4 = x² + 2x + 1

x - 5 = 0

x = 5

Problem 6 :

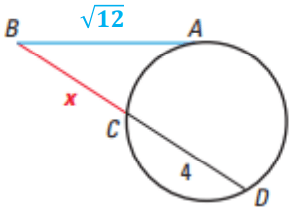
Solution :

BC ⋅ BD = (BA)²

x(x + 4) = (√12)²

x² + 4x = 12

x² + 4x - 12 = 0

(x + 6)(x - 2) = 0

x = -6 and x = 2

So, the value of x is 2.

Problem 7 :

PAB is a secant and PT is a tangent to the circle from an external point. If PT = x cm, PA = 4 cm and AB = 5 cm, find x.

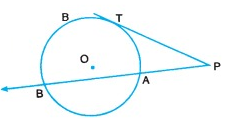
Solution:

PA ⋅ PB = (PT)²

4 ⋅ (4 + 5) = x²

4 ⋅ 9  = x²

x² = 36

x = 6

Problem 8 :

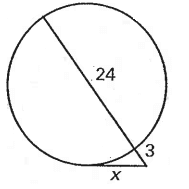
Solution :

x² = 3 (3 + 24)

x² = 3 (27)

x = √3(27)

x = 9

Problem 9 :

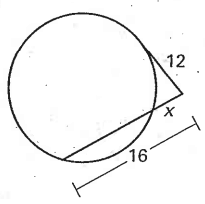
Solution :

12² = x (1 6)

x² = 3 (27)

x = √3(27)

x = 9

Problem 10 :

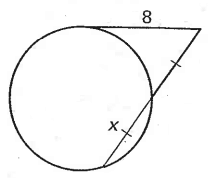
Solution :

8² = x (x + x)

8² = x (2x)

2x² = 64

x² = 32

x = 4√2