ANGLE SUBTENDED AT THE CENTER OF THE CIRCLE BY AN ARC

Let us verify the relationship between the angle subtended by an arc at the center and the angle subtended on the circumference.

Theorem :

When two angles subtended by the same arc, the angle at the center of the circle is twice the angle at the circumference

Considering the circle with center O, now placing the points A, B and C on the circumference.

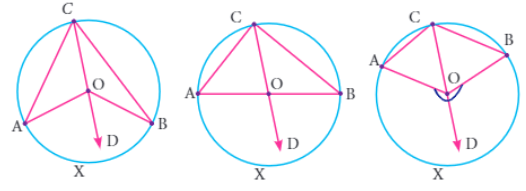
∠ACO = ∠OAC

∠BCO = ∠OBC

∠AOD = Exterior angle of the triangle

∠AOD = ∠ACO + ∠OAC  ----(1)

∠BOD = ∠BCO + ∠OBC  ----(2)

(1) + (2)

∠AOD + ∠BOD = (∠ACO + ∠OAC) + (∠BCO + ∠OBC)

∠AOB = (∠ACO + ∠OAC) + (∠BCO + ∠OBC)

∠AOB = 2∠OCA + 2∠OCB

∠AOB = 2(∠OCA + ∠OCB)

∠AOB = 2∠ACB

In each of the following figures, O is the center of the circle. Calculate the values of x and justify your answer.

Problem 1 :

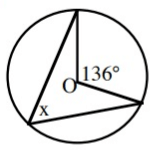
Solution :

∠x is the angle subtended at the circumference. 136˚ is the angle at the center.

So,

136 = 2x

x = 136/2

x = 68

Problem 2 :

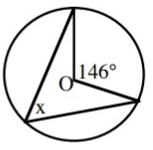
Solution :

∠x is the angle subtended at the circumference. 146˚ is the angle at the center.

So,

2x = 146˚

x = 146/2

x = 73˚

Problem 3 :

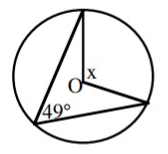
Solution :

The central angle of the same arc is twice the inscribed angle.

x = 2(49˚)

x = 98˚

Problem 4 :

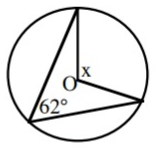
Solution :

The central angle of the same arc is twice the inscribed angle.

x = 2(62˚)

x = 124˚

Problem 5 :

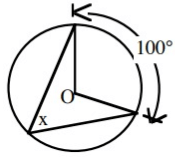
Solution :

From the figure, the angle created by the arc is 100˚.

The inscribed angel is equal to half of the central angel.

x = 100˚/2

x = 50˚

Problem 6 :

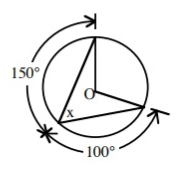
Solution :

From the figure, the angle left over is

= 360 - (150+ 100)

= 360 - 250

= 110

The inscribed angel is equal to half of the central angel.

x = 110˚/2

x = 55˚

Problem 7 :

P, Q and R are points on the circumference of a circle, center O. Angle PRQ = 64, SP and SQ are tangents to the circle at the points P and Q respectively. Work out the size of angle.

i) ∠PSQ     ii)  ∠POS        iii)  ∠QSO

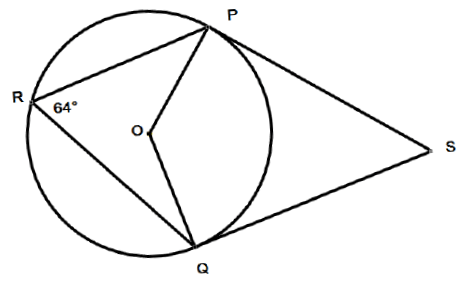
Solution :

∠POQ = 2∠PRQ

∠POQ = 2(64)

∠POQ = 128

i) Finding ∠PSQ :

Opposite angles in a quadrilateral is supplementary.

∠POQ + ∠PSQ = 180

128 + ∠PSQ = 180

∠PSQ = 180 - 128

∠PSQ = 180 - 128

∠PSQ = 52

ii) Finding ∠POS :

In triangle POS :

∠POS + ∠PSO + ∠SPO = 180 ----(1)

∠POS = ∠PSQ/2(Angle bisector)

∠POS = 52/2

∠POS = 26

Applying this value in (1), we get

ii) Finding ∠QSO :

26 + ∠PSO + 90 = 180

116 + ∠PSO = 180

∠PSO = 180 - 116

∠PSO = 64

∠QSO = 64