INSCRIBED ANGLE AND INTERCEPTED ARC OF CIRCLE

What is inscribed angle ?

Angle whose vertex is on the circle ang whose sides are chords of a circle.

Intercepted arc ?

The arc that lies between two chords on the inscribed angle.

Measure of an inscribed angle is half of its intercepted arc.

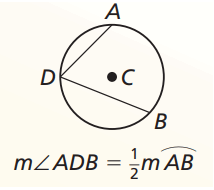
Find the measure of angle indicated.

Problem 1 :

Find ∠G

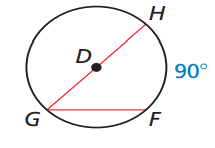
Solution :

∠HGF = 1/2 arc HF

∠HGF = (1/2) 90

∠HGF = 45

Problem 2 :

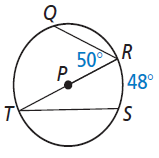
Solution :

∠RTS = 1/2 arc RS

∠RTS = (1/2) 48

∠RTS = 24

Problem 3 :

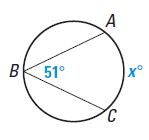
Solution :

∠ABC = 1/2 arc AC

51 = (1/2) x

x = 51(2)

x = 102

Problem 4 :

Find measure of arc TV.

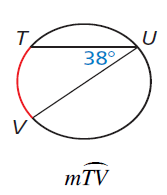
Solution :

∠TUV = 1/2 arc TV

38 = 1/2 arc TV

measure of arc TV = 2(38)

measure of arc TV = 76

Problem 5 :

Find measure of arc RS and m∠STR. What do you notice about m∠STR and m∠RUS.

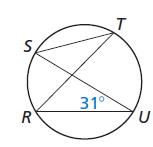
Solution :

m∠RUS lies between chords SU and RU.

m∠RUS = 1/2 of measure of arc RS

31 = 1/2 of measure of arc RS ----(1)

m∠RTS lies between chords ST and RT.

m∠RTS = 1/2 of measure of arc RS

Applying the value of 1/2 of measure of arc RS in (1), we get

m∠RTS = 31

m∠RTS and m∠RUS are equal.

Problem 6 :

Find the following.

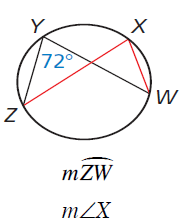
Solution :

∠ZYW = angle between ZY and YW

∠ZXW = angle between ZX and XW

∠ZYW = (1/2) measure of arc ZW

72 = (1/2) measure of arc ZW

Measure of arc ZW = 72(2)

Measure of arc ZW = 144

∠ZXW = (1/2) measure of arc ZW

∠ZXW = (1/2) 144

∠ZXW = 72

Problem 7 :

Find the values of x and y.

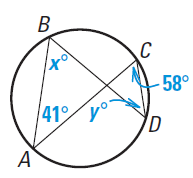
Solution :

∠ABD = ∠ACD (lies between the same arc AD)

x = 58

∠CDB = ∠BAC (lies between the same arc BC).

y = 41

Problem 8 :

Find ∠BAC

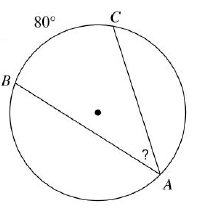
Solution :

∠BAC = (1/2) measure of arc CD

∠BAC = (1/2) (80)

∠BAC = 40

Problem 9 :

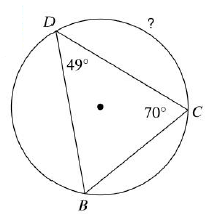
Solution :

In the triangle BDC,

∠B + ∠D + ∠C = 180

∠B + 49 + 70 = 180

∠B = 180 - 119

∠B = 61

∠DBC = (1/2) of measure of arc DC

61 = (1/2) of measure of arc DC

Measure of arc DC = 61(2)  ==> 132.

Problem 10 :

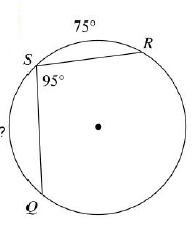
Solution :

∠RSQ = 1/2 measure of arc QR

95 = 1/2 measure of arc QR

Measures of arc QR = 95(2)

Measures of arc QR = 190

Measure of arc QR + Measure of arc RS + Measure of arc SQ = 360

190 + 75 + Measure of arc SQ = 360

Measure of arc SQ = 360 - 190 - 75

Measure of arc SQ = 95