PROBLEMS ON INTERSECTING CHORDS INSIDE A CIRCLE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
If two chords intersect inside a circle, then the measure of each angle
formed is one half the sum of the measures of the arcs intercepted by the angle
and its vertical angle.
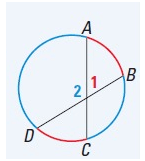
m∠1 = 1/2(mCD + mAB),
m∠1 = 1/2(mAD + mBC)
Find the
value of x.
Problem 1 :
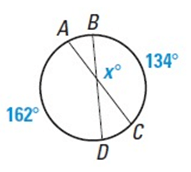
Solution :
x˚ = 1/2(mAD + mBC)
x˚ = 1/2(162˚ + 134˚)
x = 1/2(296)
x = 148
Problem 2 :
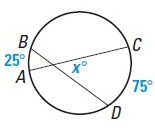
Solution :
x˚ = 1/2(mAB + mCD)
x˚ = 1/2(25˚ + 75˚)
x = 1/2(100)
x = 50
Problem 3 :
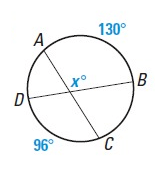
Solution :
x˚ = 1/2(mAB + mCD)
x˚ = 1/2(130˚ + 96˚)
x = 1/2(226)
x = 113
Problem 12 :
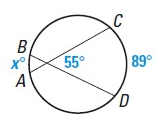
Solution :
55˚ = 1/2(mAB + mCD)
55˚ = 1/2(x + 89˚)
110˚ = x + 89
x = 110 - 89
x = 21
Problem 13:
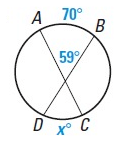
Solution :
59˚ = 1/2(mAB + mCD)
59˚ = 1/2(x + 70˚)
118˚ = x + 70
x = 118 - 70
x = 48
Problem 14 :
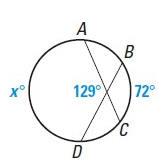
Solution :
129˚ = 1/2(mAD + mBC)
129˚ = 1/2(x + 72˚)
258˚ = x + 72
x = 258 - 72
x = 186
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling