WRITE A RULE TO DESCRIBE REFLECTION

Write a rule to describe each transformation.

Problem 1 :

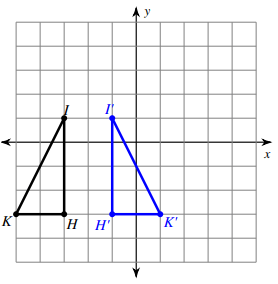
Solution :

Comparing the corresponding coordinates of two shapes,

H(-3, -3) ==> H'(-1, -3)

I(-3, 1) ==> I'(-1, 1)

K(-5, -3) ==> K'(1, -3) 

There is no change in y-coordinates, by observing the triangles from -2 on the x coordinate

H and H' are at the same distance

K and K' are at the same distance

I and I' are at the same distance

So, there is vertical line of reflection and

line of reflection at x = -2

Problem 2 :

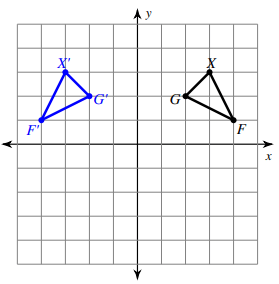
Solution :

Comparing the corresponding coordinates of two shapes,

G(2, 2) ==> G'(-2, 2)

X(3, 3) ==> X'(-3, 3)

F(4, 1) ==> F'(-4, 1) 

There is no change in y-coordinates, comparing x-coordinates, the signs alone is changed.

So,

reflection across y-axis.

Problem 3 :

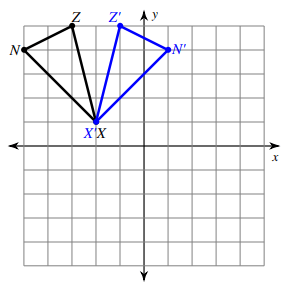
Solution :

Comparing the corresponding coordinates of two shapes,

X(-2, 1) ==> X'(-2, 1)

N(-5, 4) ==> N'(1, 4)

Z(-3, 5) ==> F'(-1, 5) 

There is no change in y-coordinates, x coordinates are changed except X. So, there may be horizontal or vertical line of reflection.

From -2 on the x-coordinate N and N' are at the same distance. Z and Z' are at the same distance. Then, there is vertical line of reflection and it is 

reflection across x = -2

Problem 4 :

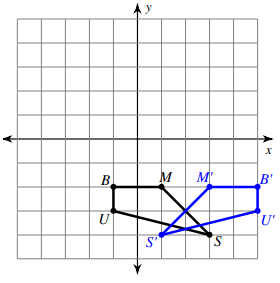
Solution :

Comparing the corresponding coordinates of two shapes,

S (3, -4) ==> S' (1, -4)

M (1, -2) ==> M' (-3, -2)

B (-1, -2) ==> B' (-5, -2)

U (-1, -3) ==> U' (-5, -3)

There is no change in y-coordinates, x coordinates are changed.

From 2 on the x-coordinate

• S and S' are at the same distance. 
• M and M' are at the same distance.
• B and B' are at the same distance.
• U and U' are at the same distance.

So,

reflection across x = 2

Problem 5 :

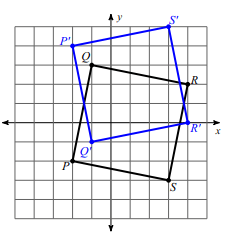
Solution :

Comparing the corresponding coordinates of two shapes,

Q (-1, 3) ==> Q' (-1, -1)

P (-2, -2) ==> P' (-2, 4)

S (3, 3) ==> S' (3, 5)

R (4, 2) ==> R' (-5, -3)

There is no change in x-coordinates, y coordinates are changed.

From 1 on the y-coordinate the vertical distance, so there may be horizontal reflection.

• Q and Q' are at the same distance. 
• P and P' are at the same distance.
• S and S' are at the same distance.
• R and R' are at the same distance.

So,

reflection across y = 1

Problem 6 :

L(0, 1), K(0, 2), J(3, 3), I(5, 1)

to

L'(0, -1), K'(0, -2), J'(3, -3), I'(5, -1)

Solution :

By comparing the corresponding coordinates

L (0, 1) ==> L' (0, -1)

K (0, 2) ==> K' (0, -2)

J (3, 3) ==> J' (3, -3)

I (5, 1) ==>  I' (5, -1)

There is no change in x-coordinate. (x, y) ==> (x, -y)

So,

Reflection across x-axis.