WORD PROBLEMS ON SURFACE AREA AND VOLUME OF CUBE

In Geometry, a Cube is a solid three-dimensional figure, which has 6 square faces, 8 vertices and 12 edges.

Volume of cube = a³

Lateral surface area = 4a²

Total surface area = 6a²

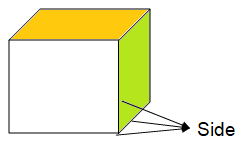
To find side length of cube from the diagonal, we use the formula

Side length = a√3

Problem 1 :

Three cubes are joined end to end forming a cuboid. If side of a cube is 2 cm, find the dimensions of the cuboid thus obtained.

Solution :

Given side of a cube = 2 cm

After joining 3 cubes,

length of cuboid = 2 × 3 = 6 cm, 

Height = 2 cm and Breadth = 2 cm

Dimension of the cuboid is 6 cm x 2 cm x 2 cm.

Problem 2 :

Find the lateral surface area of a cube, if its diagonal is √6 cm.

Solution :

Given, diagonal of the cube = √6 cm

Diagonal of the cube = √3 a

√3 a = √6

a = √6/√3

a = √2 cm

Lateral surface area of cube = 4a²

= 4 × (√2)²

= 4 × 2

= 8 cm²

Problem 3 :

Three cubes of metal whose edges are in the ratio 3 : 4 : 5 are melted down into a single cube whose diagonal is 12√3 cm. find the edges of the three cubes.

Solution :

Diagonal of the single cube = 12√3 cm

√3 a = 12√3

a = 12 cm

Volume of the single cube = sum of the volumes of the metallic cubes

a³ = (3x)³ + (4x)³ + (5x)³

(12)³ = 27x³ + 64x³ + 125x³

1738 = 216x³

x³ = 1728/216

x³ = 8

x³ = 2³

x = 2

Now, the edge of the first cube = 3(2) = 6 cm

Edge of the second cube = 4(2) = 8 cm

Edge of the third cube = 5(2) = 10 cm

Therefore, the edges of the three cubes are 6 cm, 8 cm, and 10 cm.

Problem 4 :

Volume of a cube is 5832 m³. Find the cost of painting its total surface area at the rate of $3.50 per m².

Solution :

Volume of a cube is 5832 m³

a³ = 5832 m³

a = 5832

a = 18 m

Total surface area = 6 × a²

= 6 × 324 = 1944 m²

Cost of painting at 3.50 per m² = 1944 × 3.50

= 6804

Hence, the cost of painting is $6804

Problem 5 :

The cube has a surface area of 216 dm². Calculate:

a)   The area of one wall,

b)   Edge length,

c)   Cube volume.

Solution :

The cube has a surface area of 216 dm²