FIND LATERAL AND TOTAL SURFACE AREA OF RECTANGULAR PRISM

In geometry, a rectangular prism can be defined as a 3-dimensional solid shape which has six faces that are rectangles. A rectangular prism is also a cuboid.

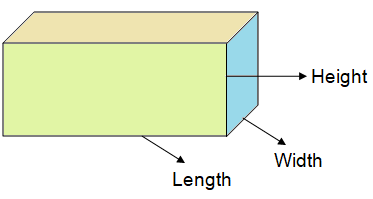
What is lateral surface area ?

The lateral surface of an object is all of the sides of the object, excluding its base and top. The lateral surface area is the area of the lateral surface.

What is total surface area ?

The total surface of an object is all of the sides of the object, including its base and top. 

Lateral surface area of rectangular prism = 2h(l + w)

Total surface area of rectangular prism = 2(lw + wh + hl)

Find the 

(i) Lateral surface area and 

(ii)  Total surface area of the following rectangular prism.

Problem 1 :

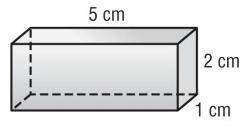
Solution :

From the prism,

l = 5 cm, w = 1 cm and h = 2 cm

(i) Lateral surface area = 2h (l +w)

= 2(2)(5 + 1)

= 4(6)

= 24 cm²

(ii) Total surface area of the rectangular prism

= 2(lw + lh + wh)

= 2 [(5 × 1) + (5 × 2) + (1 × 2)]

= 2(5 + 10 + 2)

= 2(17)

= 34 cm²

Problem 2 :

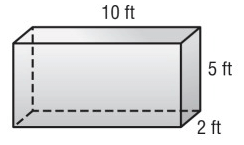
Solution :

From the prism,

l = 10 ft, w = 2 ft and h = 5 ft

(i) Lateral surface area = 2h (l +w)

= 2(5)(10 + 2)

= 10(12)

= 120 ft²

(ii)  Total surface area of the rectangular prism

= 2(lw + lh + wh)

= 2 [(10 × 2) + (10 × 5) + (2 × 5)]

= 2(20 + 50 + 10)

= 2(80)

= 160 ft²

Problem 3 :

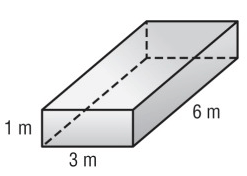
Solution :

From the prism,

l = 6 m, w = 3 m and h = 1 m

(i) Lateral surface area = 2h (l +w)

= 2(1)(6 + 3)

= 2(9)

= 18 m²

(ii)  Total surface area of the rectangular prism

= 2(lw + lh + wh)

= 2 [(3 × 1) + (3 × 6) + (1 × 6)]

= 2(3 + 18 + 6)

= 2(27)

= 54 m²

Problem 4 :

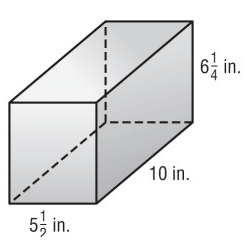
Solution :

From the prism,

l = 10 in, w = 11/2 in and h = 25/4 in

(i) Lateral surface area = 2h (l + w)

= 2(25/4)(10 + 11/2)

= (25/2)(31/2)

= 193.75 ft²

(ii)  Total surface area of the rectangular prism

= 2(lw + lh + wh)

= 2 [(11/2 × 10) + (25/4 × 11/2) + (10 × 25/4)]

= 2(55 + 34.375 + 62.5)

= 2(151.87)

= 303.75 ft²

Problem 5 : 

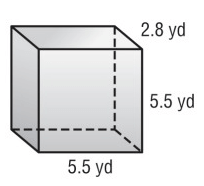
Solution :

From the prism,

l = 5.5 yd in, w = 2.8 yd and h = 5.5 yd

(i) Lateral surface area = 2h (l + w)

= 2(5.5)(5.5 + 2.8)

= 11(8.3)

= 91.3 yd²

(ii)  Total surface area of the rectangular prism

= 2(lw + lh + wh)

= 2 [(5.5 × 2.8) + (5.5 × 5.5) + (2.8 × 5.5)]

= 2(15.4+ 30.25 + 15.4)

= 2(61.05)

= 122.1 yd²

Problem 6 : 

A rectangular room is 12 feet by 21 feet. The walls are 8 feet tall. Paint is sold in one gallon containers. If a gallon of paint covers 450 sqaure feet, how many gallons of paint should poloma buy to paint the walls of the room ?

Solution :

Dimensions of room :

Length = 12 feet, width = 21 feet and height = 8 feet

Number of walls = 4

Surface area of rectangular room = 2h(l + w)

= 2 x 8 x (12 + 21)

= 16 x 33

= 528 square feet

1 gallon of paint will cover 450 square feet

Number of gallons = 528/450

= 1.17

Approximately 2 gallons of paint is needed.

Problem 7 : 

The scale factor of prism X to prism Y is 2/3. What is the ratio of the surface area of prism X to the surface area of prism Y.

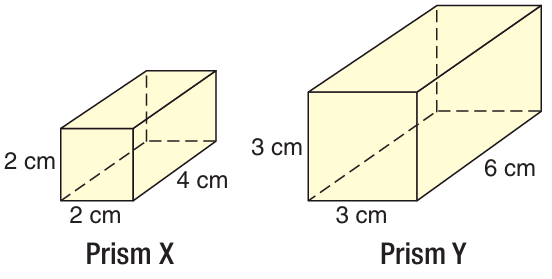
Solution :

Dimension of prism X :

length = 4 cm, width = 2 cm and height = 2 cm

Surface of prims X = 2h(l + w)

= 2 x 2 (4 + 2)

= 4 x 6

= 24 cm²

Dimension of prism Y :

length = 6 cm, width = 3 cm and height = 3 cm

Surface of prims X = 2h(l + w)

= 2 x 3 (3 + 6)

= 6 x 9

= 54 cm²

Ratio between surface area of prism X to prism Y :

= 24/54

= 4/9

So, the required ratio is 4 : 9.

Problem 8 : 

The greater the surface area of an ice block, the faster it will melt. Which will melt faster, the bigger block or the three smaller blocks? Explain your reasoning.

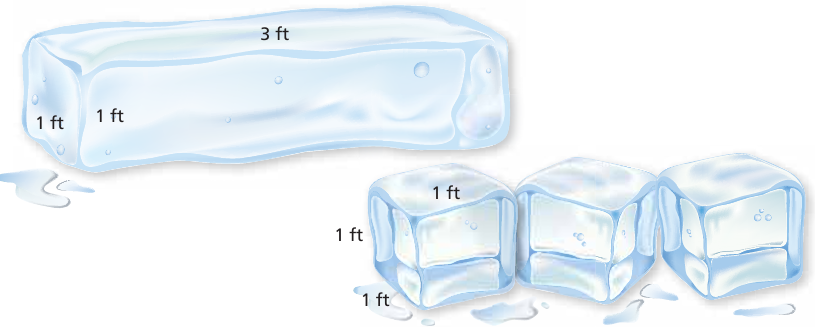
Solution :

Surface area of rectangular prism :

length = 3 ft, width = 1 ft and height = 1 ft

Total surface area = 2(lw + wh + hl)

= 2(3⋅1 + 1⋅1 + 1⋅3)

= 2(3 + 1 + 3)

= 2(7)

= 14 square feet

Surface area of 3 cubes :

Side length = 1 ft

Total surface area = 4a²

= 3(4⋅1²)

= 3(4)

= 12 square feet

So, 3 small cubes will melt faster.