VOLUME OF TRIANGULAR PRISM

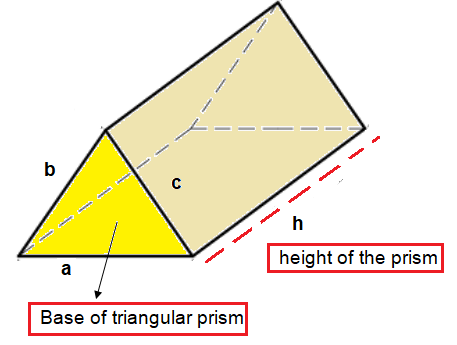
Volume of triangular prism = Base area x height

Problem 1 :

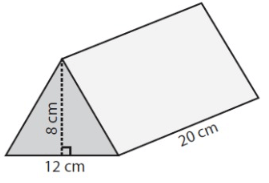
Find the volume of the triangular prism given below.

Solution :

Base area = (1/2) x base x height

= (1/2) x 12 x 8

= 48

Volume = baes area x height of the prism

= 48 x 20

V = 960 cm³

Problem 2 :

Find the 

(i) Total surface area

(ii) Volume

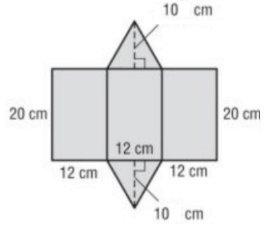
of the triangular prism given below.

Solution :

(ii) Total surface area :

Area of triangle = 2(1/2) × b × h

= 12 × 10

Area of triangle = 120 cm² --- > (1)

Area of rectangle = b × h

= 20 × 12

= 240 cm²  

Area of three rectangle = 3 × b × h

= 3 × 240

= 720 cm² --- > (2)

Add (1) & (2)

Total surface area = 120 + 720

= 840 cm²

So, surface area of triangular prism = 840 cm²

(ii)  Volume = Base area x height

= 120 x 20

= 2400 cm³

Problem 3 :

The height of a triangular prism is 6 cm and its base is an equilateral triangle of side 5 cm. Find the volume of the prism.

Solution :

Volume of triangular prism (V) = Base area x height

Base is in the shape of equilateral triangle,

Area of equilateral triangle = √3/4 × a²

So, volume of triangular prism = 64.95 cm³

Problem 4 :

A right prism stands on a base which is a right triangle with legs 3 cm and 4 cm. find the volume of the prism if its height is 9 cm.

Solution :

Given, side a = 3 cm and b = 4 cm

Using Pythagoras theorem,

Area of triangle = √s(s - a)(s - b)(s - c)

= √6 (6 - 3)(6 - 4)(6 - 5)

= √6(3)(2)(1)

= √36

= 6 cm²

Volume of right prism = Base area × height

= 6 × 9

= 54 cm³

So, volume of triangular prism = 54 cm³

Problem 5 :

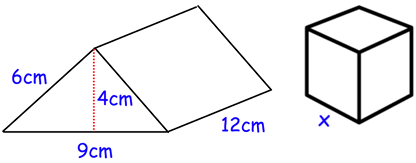
The solid triangular prism shown below is made from metal. The prism is melted down and the metal is used to create a solid cube. Find the side length of the cube.

Solution :

volume of triangular prism = volume of cube

(1/2) x 9 ⋅ 4 ⋅ 12  = x ⋅ x ⋅ x

9 ⋅ 2 ⋅ 12  = x³

216 = x³

6³ = x³

x = 6 cm

So, the side length of the cube is 6 cm.

Problem 6 :

Use the appropriate formula to solve for the missing measurement: Find the height of a triangular prism if it has length of 14ft, a base of 8 ft, and a volume of 336 ft³.

Solution :

height = 14 ft and base = 8 ft

Volume = 336 ft³

(1/2) x 14 x 8 x height of the triangular prism = 336

7 x 8 x height of triangular prism = 336

height of triangular prism = 336/56

= 6 ft

So, height of the triangular prism is 6 ft.

Problem 7 :

a) Calculate the volume of the triangular prism.

b) The slice is 1/2 of a rectangular cake. What was the volume of the original cake?

Solution :

a) Volume of triangular prism = base area x height

= (1/2) x 12 x 20 x 6

= 36 x 20

= 720 square cm

b) Volume of original cake = 2 (volume of half of the cake)

= 2(720)

= 1440 square cm.

Problem 8 :

The diagram shows a triangular prism. The cross-section of the prism is a right angled triangle. The volume of the prism is 198 cm³ Calculate the value of x

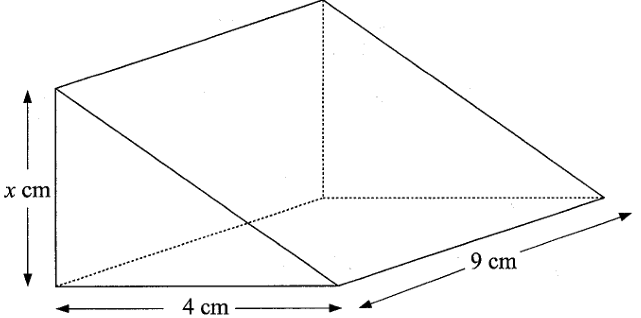
Solution :

Volume of prism = 198

(1/2) ⋅ 4 ⋅ 9 ⋅ x = 198

2 ⋅ 9 ⋅ x = 198

18x = 198

x = 198/18

x = 11 cm

So, the height of the triangular prism is 11 cm.

Problem 9 :

Here is a triangular prism.

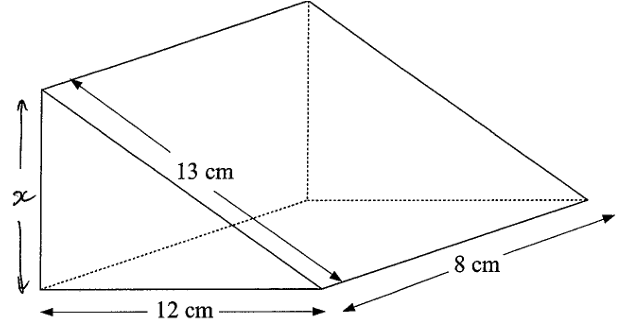
The diagram shows a triangular prism. The cross-section of the prism is a right angled triangle. Calculate the volume of the prism.

Solution :

By observing the base of the triangular prism, it is right triangle.

13² = x² + 12²

169 = x² + 144

x² = 169 - 144

x² = 25

x = 5 cm

So, height of the base triangle is 5 cm.

Height of the prism = 8 cm

Volume of the triangular prism = (1/2) ⋅ 12 ⋅ 5 ⋅ 8

= 6 ⋅ 5 ⋅ 8

= 240 cm²

So, the volume of given triangular prism is 240 cm².