VOLUME OF TRIANGULAR PRISM WORD PROBLEMS

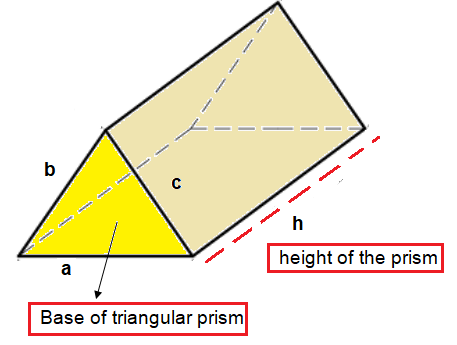
Volume of triangular prism = Base area x height

Problem 1 :

The height of a triangular prism is 6 cm and its base is an equilateral triangle of side 5 cm. Find the volume of the prism.

Solution :

Volume of triangular prism (V) = Base area x height

Base is in the shape of equilateral triangle,

Area of equilateral triangle = √3/4 × a²

So, volume of triangular prism = 64.95 cm³

Problem 2 :

A right prism stands on a base which is a right triangle with legs 3 cm and 4 cm. find the volume of the prism if its height is 9 cm.

Solution :

Given, side a = 3 cm and b = 4 cm

Using Pythagoras theorem,

Area of triangle = √s(s - a)(s - b)(s - c)

= √6 (6 - 3)(6 - 4)(6 - 5)

= √6(3)(2)(1)

= √36

= 6 cm²

Volume of right prism = Base area × height

= 6 × 9

= 54 cm³

So, volume of triangular prism = 54 cm³

Problem 3:

The base of a right prism is a right triangle with legs 6 and 8 cm. if the volume of the prism be 192 cu cm. find the height of the prism.

Solution :

Side a = 6 cm and b = 8 cm

Using Pythagoras theorem

Perimeter of a triangle = (6 + 8 + 10) / 2

= 24/2

= 12 cm

Area of triangle = √s(s - a)(s - b)(s - c)

= √12 (12 - 6)(12 - 8)(12 - 10)

= √12(6)(4)(2)

= √576

= 24 cm²

Volume of right prism = Base area × height

192 = 24 × height

Height = 192/24

Height = 8 cm

So, height of triangular prism = 8 cm.

Problem 4:

The base of a right prism is a triangle with base 12 cm and height 6 cm. find the volume of the prism if its height is 7 cm.

Solution :

Given, base of the triangle = 12 cm

Height = 6 cm

Area base = 1/2 × 12 × 6

= 36 cm²

Height of the prism h = 7 cm

Volume of triangular prism V = A × h

= 36 × 7

V = 252 cm³

So, the volume of triangular prism V = 252 cm³

Problem 5 :

The height of a triangular prism is 8 cm and its base is an equilateral triangle of side 4 cm. Find the volume of the prism.

Solution :

Volume of triangular prism V = A × h

So, volume of triangular prism = 55.42 cm³

Problem 6 :

The height of a right prism is 12 cm and its base is a triangle with 9 cm as base and height 5 cm. Find the volume of the prism.

Solution :

Base of the triangle prism = 9 cm

Height = 12 cm

Area base = 1/2 × 9 × 12

= 54 cm²

Height of the prism h = 5 cm

Volume of triangular prism V = A × h

= 54 × 5

V = 270 cm³

So, the volume of triangular prism V = 270 cm³

Problem 7 :

The base of a right prism is a right triangle with legs 12 and 5 cm. if the volume of the prism be 210 cu cm. find the height of the prism.

Solution :

Side a = 12 cm and b = 5 cm

Using Pythagoras theorem

a² + b² = c²

12² + 5² = c²

c = √(144 + 25)

c = √169

c = 13 cm

Perimeter of a triangle = (12 + 5 + 13) / 2

= 30/2

= 15 cm

Area of triangle = √ s(s - a)(s - b)(s - c)

= √ 15 (15 - 12)(15 - 5)(15 - 13)

= √ 15(3)(10)(2)

= √900

= 30 cm²

Volume of right prism = Base area × height

210 = 30 × height

Height = 210/30

Height = 7 cm

So, height of triangular prism = 7 cm.

Problem 8 :

A right prism base is a triangle whose sides are 6 cm, 8 cm and 10 cm. Find the volume of the prism if its height is 12 cm.

Solution :

side a = 6 cm and b = 8 cm and c = 10 cm

Perimeter of a triangle = (6 + 8 + 10) / 2

= 24/2

= 12 cm

Area of triangle = √s(s - a)(s - b)(s - c)

= √12 (12 - 6)(12 - 8)(12 - 10)

= √12(6)(4)(2)

= √576

= 24 cm²

Volume of right prism = Base area × height

 = 24 × 12

V = 288 cm³

So, volume of the triangular prism = 288 cm³.

Problem 9 :

The height of a right prism is 15 m and its base is a triangle. If the volume of the prism is 187.5 cu m, find the area of the base triangle.

Solution : 

Height of prism h = 15 m

Volume V = 187.5 cu m

Volume of triangular prism V = A × h

Area of base of triangular prism A = V/h

= 187.5/15

V = 12.5 m²

So, Area of base of triangle = 12.5 m²

Problem 10 :

A right prism is a triangle whose sides are 18 cm, 20 cm and 34 cm. find the volume of the prism if its height is 6 cm.

Solution :

Given, side a = 18 cm and b = 20 cm and c = 34 cm

Perimeter of a triangle = (18 + 20 + 34) / 2

= 72/2

= 36 cm

Area of triangle = √s(s - a)(s - b)(s - c)

= √36 (36 - 18)(36 - 20)(36 - 34)

= √36(18)(16)(2)

= √20736

= 144 cm²

Volume of right prism = Base area × height

 = 144 × 6

V = 864 cm³

So, volume of the triangular prism = 864 cm³.