HOW TO FIND SIDE LENGTH OF CUBE FROM DIAGONAL

Deriving the Length of the Diagonal

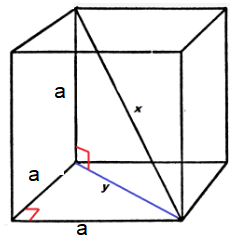
In a cube each face will be square,

a² + a² = y²

2a² = y²

y = √2a²

y = a√2

Then,

a² + y² = x²

a² + (a√2)² = x²

a² + a²(2) = x²

a² + 2a² = x²

3a² = x²

x = √3a²

x = a√3

So, length of the diagonal of a cube is a√3.

Here a is side length.

Problem 1 :

Find the value of x.

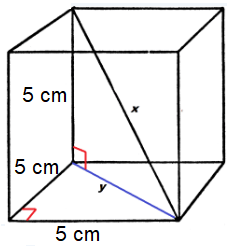
Solution :

Problem 2 :

Find the lateral surface area of a cube, if its diagonal is √6 cm.

Solution :

Given, diagonal of the cube = √6 cm

Diagonal of the cube = √3 a

√3 a = √6

a = √6/√3

a = √2 cm

Lateral surface area of cube = 4a²

= 4 × (√2)²

= 4 × 2

= 8 cm²

Problem 3 :

The side length of a cube is 5 meters. What is the length of its diagonal across one of the faces?

Solution :

Side length of cube (a) = 5 m

Length of the diagonal of a cube = a√3

length of the diagonal = 5√3

Problem 4 :

Find the length of the face diagonal of a cube when the side measures 9 units. Use the diagonal face formula of a cube.

Solution :

Length of one face diagonal of cube = a√2

Side length of the cube = 9 units

length of one face of diagonal = 9√2