FIND HEIGHT AND SLANT HEIGHT OF THE CONE WHEN SURFACE IS GIVEN

Find the slant height (h) and slant height (l) of the cone given below. Total surface area is given.

Problem 1 :

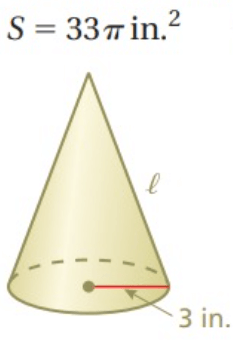
Solution :

Surface area of cone = 33π

π r(l + r) = 33π

Applying the value of r, we get

3(l + 3) = 33

Dividing by 3.

l + 3 = 11

Subtracting 3 on both sides.

l = 11 - 3

l = 8

h = √l² - r²

h = √8² - 3²

h = √(64 - 9)

h = √55

So, required height = √55 inches and slant height = 8 inches.

Problem 2 :

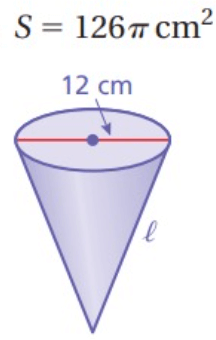
Solution :

Surface area of cone = 126π

Diameter = 12 cm

radius = 6 cm

π r(l + r) = 126π

Applying the value of r, we get

6(l + 6) = 126

Dividing by 6.

l + 6 = 21

Subtracting 6 on both sides.

l = 21 - 6

l = 15

h = √l² - r²

h = √15² - 6²

h = √(225 - 36)

h = √189

So, required height = 15 cm and slant height = √189 cm.

Problem 3 :

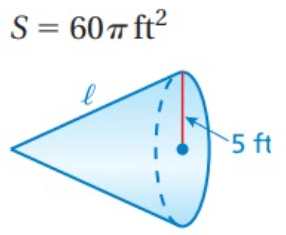
Solution :

Surface area of cone = π

radius = 5 ft

π r(l + r) = 60π

Applying the value of r, we get

5(l + 5) = 60

Dividing by 5.

l + 5 = 12

Subtracting 5 on both sides.

l = 21 - 5

l = 16

h = √16² - 5²

h = √256 - 25

h = √231

So, the required slant height is 16 ft and height is √231 ft.

Problem 4 :

The curved surface area of a cone is 12320 sq. cm, if the radius of its base is 56 cm, then its height is

a) 24 cm        b) 25 cm         c) 42 cm         d) 45 cm

Solution :

Curved surface area of cone = 12320 sq. cm

radius (r) = 56 cm, height (h) = ?

π r l = 12320

3.14 ⋅ 56 ⋅ l = 12320

l = 12320 / (3.14 ⋅ 56)

l = 70

h = √l² - r²

h = √70² - 56²

h = √(4900 - 3136)

h = √1764

h = 42 cm

So, option c is correct.

Problem 5 :

The radius of two similar right circular cones are 2 cm and 6 cm. the ratio of their volumes is

a) 1 : 3     b) 1 : 9      c) 9 : 1      d) 1 : 27

Solution :

Radius of two similar cones = 2x and 6x

Volume of cone = (1/3) ⋅ πr²h 

Volume of similar cones = (1/3) ⋅ πr₁²h :  (1/3) ⋅ πr₂²h

= (2x)² :  (6x)²

= 4x² : 36x²

= 1 : 9

So, option b is correct.

Problem 6 :

How much ice-cream can be put into a cone with base radius 3.5 cm and height 12 cm?

a) 176 𝑐𝑚³          b) 154 𝑐𝑚³         c) 124 𝑐𝑚³      d) 254 𝑐𝑚³

Solution :

Radius = 3.5 cm and height = 12 cm

Quantity of ice cream inside the cone = (1/3) ⋅ πr²h

= (1/3) ⋅ 3.14 ⋅ 3.5² ⋅ 12

= 3.14 ⋅ 3.5² ⋅ 4

= 153.86

Approximately154 𝑐𝑚³. Option b is correct.

Problem 7 :

Determine the volume of a conical tin having radius of the base as 30 cm and its slant height is 50 cm.

Solution :

Radius = 30 cm, slant height = 50 cm

h = √l² - r²

h = √50² - 30²

h = √(2500 - 900)

h = √1600

h = 40 cm

Volume of cone = (1/3) ⋅ πr²h

= (1/3) ⋅ 3.14 ⋅ 30² ⋅ 40

= 37680 cm³

So, the required volume is 37680 cm³.

Problem 8 :

Find the capacity in litres of a conical vessel having height 8 cm and slant height 10 cm. (take 𝜋 = 3.14)

Solution :

height of cone = 8 cm and slant height = 10 cm

Capacity of cone = (1/3) ⋅ πr²h

r = √l² - h²

r = √10² - 8²

r = √(100 - 64)

r = √36

r = 6 cm

= (1/3) ⋅ 3.14 ⋅ 6² ⋅ 8

= 301.44 cm³

1 liter = 1000 cm³

1 cm³ = 1/1000 liter

301.44 cm³ = 301.44/1000 liter

= 0.30144 liter

Problem 9 :

Once four friends Rahul, Arun, Ajay and Vijay went for a picnic at a hill station. Due to peak season they did not get a proper hotel in the city. The weather was fine so they decided to make a conical tent at a park. They were carrying 300 m² of cloth with them. As shown in the figure they made the tent with height 6 m and radius 8 m. The remaining cloth was used for the floor.

i) How much cloth was used for the tent (excluding the floor)?

ii) How much cloth was left with them?

iii) If the cost of cloth per m² is ₹150, then find the total cost for making the tent (excluding the floor)?

Solution :

Height of the tent = 6 m, radius of the tent = 8 m

i) Quantity of material used for tent = πrl

l = √r² + h²

l = √8² + 6²

l = √(64 + 36)

l = √100

l = 10 m

= 3.14 x 8 x 10

= 251.2 m²

ii) Quantity of material left = 300 - 251.2

= 48.8 m²

iii)  Cost per meter square = 150

Required cost = 251.2 x 150

= 37680