PROBLEMS ON SURFACE AREA AND VOLUME OF CYLINDER

Problem 1 :

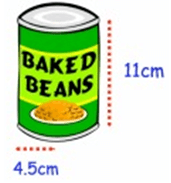
A can of baked beans has a paper label wrapped around the outside. The can has a height of 11 cm and radius of 4.5 cm. The label covers the entire height of the can. The label has a 1 cm overlap vertically so that it can be stuck together calculate the area of the label

Solution :

By observing the figure,

Radius r = 4.5 cm

Height h = 11 cm

The label has a 1 cm overlap vertically. So, height h = 12 cm

Area of the label = 2πrh

= 2 × π × 4.5 × 12

= 2 × 3.14 × 4.5 × 12

= 339.12 cm

Area of the label is 339.12 cm.

Problem 2 :

The cylinder and cube below have the same surface area.

Find the side length of the cube, x.

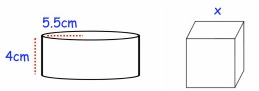
Solution :

Radius r = 5.5 cm, height h = 4 cm

Surface area of the cylinder = surface area of the cube

2πr(h + r) = 6s²

2π(5.5)(4 + 5.5) = 6(x²)

(11π)(9.5) = 6x²

104.5π = 6x²

104.5π/6 = x²

17.4π =x²

17.4 × 3.14 =x²

54.636 = x²

√54.636 = x

7.39 cm = x

So, length of cube is 7.39 cm.

Problem 3 :

A tank on the road roller is filled with water to make the roller heavy. The tank is a cylinder that has a height of 6 feet and a radius of 2 feet. One cubic foot of water weighs 62.5 pounds. Find the weight of the water in the tank

Solution :

height of the tank = 6 feet, radius = 2 feet

Volume v = πr²h

= 3.14 × (2)² × 6

= 3.14 × 4 × 6

= 75.36 ft

So, the weight of the water in the tank is 75.36 ft. 

One cubic foot of water weighs = 62.5 pounds

= 62.5 × 75.36

= 4710 pounds.

Problem 4 :

A cylinder has a surface area of 1850 square meters and a radius of 9 meters. Estimate the volume of the cylinder to the nearest whole number.

Solution :

Surface area of the cylinder = 1850 square meters

Radius = 9 meters  

Surface area of the cylinder = 2πrh

1850 = 2 × 22/7 × 9 × h

1850 × 1/2 × 7/22 × 1/9 = h

32.7 = h

Volume of the cylinder V = πr²h

= 22/7 × (9)² × 32.7

= 8316.918 cubic meters

Problem 5 :

Water flows at 2 feet per second through a pipe with a diameter of 8 inches. A cylindrical tank with a diameter of 15 feet and a height of 6 feet collects the water.

a) what is the volume, in cubic inches, of water flowing out of the pipe every second.

b) What is the height, in inches, of the water in the tank after 5 minutes?

c) How many minutes will it take to fill 75% of the tank?

Solution :

Diameter d = 8 feet ==> radius = 4 feet

height (h) = 2 feet ==> 24 inches

(a)  Volume of water flows out every second = πr²h

=  π x 4² x 24

= 384π

Using π = 3.14, we get

= 1206 cubic inches

(b)  quantity of water in the cylindrical tank after 5 minutes : 

5 minutes = 300 seconds

Quantity of water = 384π x 300

= 115200π

Volume of water in cylindrical tank = 115200π

πr²h = 115200π

r = 15/2 ==> 7.5 feet ==> 90 inches

π(90)² h = 115200π

h = 115200/8100

h = 14.2 inches

c) How many minutes will it take to fill 75% of the tank?

Capacity of the tank = πr²h

r = 90 inches, h = 6x12 ==> 72 inches

= π(90)²(72)

= 583200π

75% of the capacity = 0.75 (583200π)

= 437400π

Volume of water in 1 second = 384π

= 437400π/384π

= 1140 seconds

Converting seconds to minutes,

= 1140/60

= 19 minutes 

Problem 6 :

A cylindrical swimming pool has a diameter of 16 feet and a height of 4 feet. About how many gallons of water can the pool contain? Round your answer to the nearest whole number. (1 ft³ ≈ 7.5 gal)

Solution :

Diameter (d) = 16 feet, radius r = 8

Height h = 4 feet

Volume of the cylinder V = πr²h

= 3.14 × 8² × 4

= 3.14 × 64 × 4

= 803.8 ft

1 ft³ = 7.5 gallon

Quantity of water that pool can contain = 7.5 × 803.8

= 6028.5 gallons

= 6029 gallons