FIND VOLUME OF CUBE GIVEN SURFACE AREA

In Geometry, a Cube is a solid three-dimensional figure, which has 6 square faces, 8 vertices and 12 edges.

Volume of cube = a³

To find side length of cube from the diagonal, we use the formula

Side length = a√3

Problem 1 :

Calculate the volume of the cube if its surface is 150 cm².

Solution :

Let ‘a’ be the side of the cube.

Surface area of cube = 150 cm²

6a² = 150

a² = 25

a = 5

Volume of the cube = a³

= 5³

V = 125 cm³

Problem 2 :

The cube has a surface of 600 cm². What is its volume?

Solution :

Given, Surface area of cube = 6a²

Let side of cube = a cm

Problem 3 :

We make a box in the shape of a cube with an edge of 12 cm. how many cm² of sheet metal do we need to create a box if we do not make the lid?

Solution :

Edge a = 12 cm

Surface area of cube = 5 × a²

= 5 × 12

S = 720 cm²

Problem 4 :

If we reduce the length of the cube edge by 30%, this reduced cube has an area of 1176 cm². Specify the edge length and volume of the original cube.

Solution :

Let a be the length of the original cube.

This side length is going to be reduced by 30%. So length of new cube will be 70% of the original cube.

6a² = surface area of the cube

Surface area of new cube = 6(0.70a)²

= 2.94 a²

2.94a² = 1176

a² = 1176/2.94

a² = 400

a = √400

a = 20

side length of cube is 20 cm.

Volume of cube = a³

= 20³

= 8000

So, the volume of cube V = 8000 cm³

Problem 5 :

How can you change the edge length of a cube so that the volume is reduced by 40%?

Solution :

Let a be the side length of the cube.

Volume of cube which has side length a cm

= a³

Volume of new cube = 140% of volume of old cube

= 60% of a³

Let b be the side length of new cube.

b³ = 60% of a³

b³ = 0.6 a³

b = 0.843 a

So, side length of new cube is 0.843 a.

Problem 6 :

A pyramid with a square base has a volume of 120 cubic meters and a height of 10 meters. Find the side length of the square base.

Solution :

Volume of square base pyramid = (1/3) x base area x height

Volume of pyramid = 120 cubic meters

height = 10 meters

120 = (1/3) x base area x 10

(120 x 3)/10 = base area

base area = 36

Area of square = 36

Let a be the side length of the square.

x² = 36

x = 6 cm

So, the side length of the square base is 6 cm.

Problem 7 :

A pyramid with a square base has a volume of 912 cubic feet and a height of 19 feet. Find the side length of the square base.

Solution :

Volume of square base pyramid = (1/3) x base area x height

Volume of pyramid = 912 cubic feet

height = 19 feet

912 = (1/3) x base area x 19

(912 x 3)/19 = base area

base area = 144

Area of square = 144

Let a be the side length of the square.

x² = 144

x = 12 feet

So, the side length of the square base is 12 feet.

Problem 8 :

A cube with a surface area of 96 square centimeters is shown. Eight cubes like the one shown are combined to create a larger cube. What is the volume, in cubic centimeters, of the new cube?

Solution :

Surface area of cube = 6a²

6a² = 96 square cm

a² = 96/6

a² = 16

a = 4 cm

So, side length of the square is 4 cm.

Volume of 8 cubes = 8a³

= 8(4)³

= 8 (64)

= 512 cm³

Problem 9 :

Find the volume of the composite solid below.

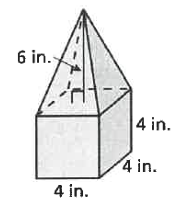
Solution :

Volume of the figure = Base area  x height

Base area = 4 x 4

= 16 square inches

Height = 6 inches

= 16 x 6

= 96 cubic inches

So, the volume of the shown figure is 96 cubic inches.

Problem 10 :

Two pyramids with square bases have the same volume. One pyramid has a height of 6 centimeters and the area of the base is 36 square centimeters.

a. What is the volume of the pyramids?

b. The base of the other pyramid has a side length of 3 centimeters. What is the height of this pyramid?

Solution :

a) Base area of one pyramid = 36 square cm

height = 6 cm

Volume of the pyramid = 36 x 6

= 216 cubic cm

b) Base length of other pyramid = 3 cm

Volume = base area x height

216 = 3 x 3 x height

216 = 9 x height

height = 216 / 9

= 24 cm

So, the height of the other pyramid is 24 cm.