SURFACE AREA OF SQUARE BASE PYRAMID

A square pyramid is a pyramid that has a square base and four lateral faces. A Pyramid is a polyhedron that has a base and 3 or greater triangular faces that meet at a point above the base (the apex).

A square pyramid is a three-dimensional shape that has a total of five faces, hence called a pentahedron. 

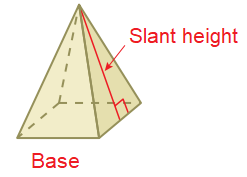
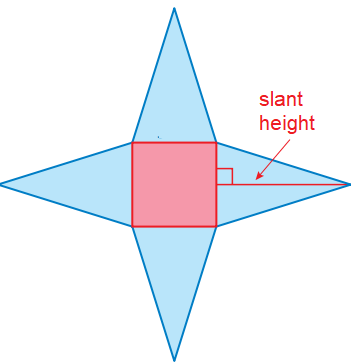
To find surface area of square pyramid, we have two different ways.

• Find sum of areas of all sides
• Using formula

Find the surface area of the square pyramid given below.

Example 1 :

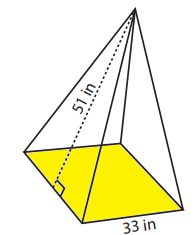
Solution :

Method 1 :

Required surface area = Area of base + 4 Area of triangles

Area of base = 33² ==> 1089 in²

Area of triangle = (1/2) x base x height

Area around the shape = 4 x (1/2) x base x height

= 2 x 33 x 51

= 3366 in²

Surface area = 1089 + 3366

= 4455 in²

Method 2 :

Surface area of square pyramid = A + 2 s l

A= area of base, p = side length and l = slant height

= 33² + 2 x 33 x 51

= 1089 + 3366

= 4455 in²

Example 2 :

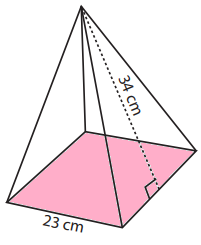
Solution :

Required surface area = Area of base + 4 Area of triangles

Area of base = 23² ==> 529 cm²

Area of triangle = (1/2) x base x height

Area around the shape = 4 x (1/2) x base x height

= 2 x 34 x 23

= 1564 cm²

Surface area = 529 + 1564

= 2093 cm²

Example 3 :

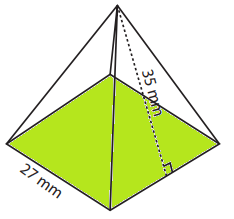
Solution :

Required surface area = Area of base + 4 Area of triangles

Area of base = 27² ==> 729 mm²

Area of triangle = (1/2) x base x height

Area around the shape = 4 x (1/2) x base x height

= 2 x 27 x 35

= 1890 mm²

Surface area = 729 + 1890

= 2619 mm²

Example 4 :

A roof is shaped like a square pyramid. One bundle of shingles covers 25 square feet. How many bundles should you buy to cover the roof ?

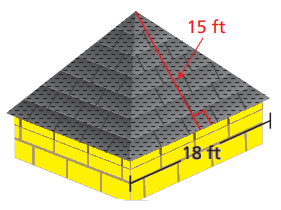
Solution :

Surface area = 2 x 18 x 15

= 540 square feet

Because one bundle of shingles covers 25 square feet, it will take

540 ÷ 25 = 21.6

bundles to cover the roof. So, you should buy 22 bundles of shingles

Example 5 :

Originally, Khafre’s Pyramid had a height of about 144 meters and a volume of about 2,218,800 cubic meters. Find the side length of the square base.

Solution :

Height = 144 meters

Volume of square base pyramid = 2,218,800 cubic meters

(1/3) x Base area x height = 2,218,800

Base area x 144 = 2,218,800 x 3

Base area = (2,218,800 x 3)/144

= 46225

Let x be the side length of square.

x² = 46225

x = √46225

x = 215 meter

Example 6 :

Pyramid A and pyramid B are similar. Find the volume of pyramid B.

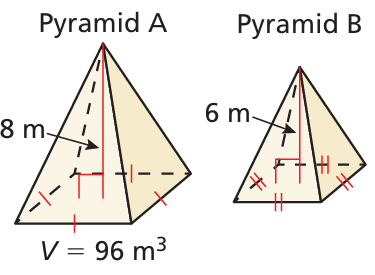
Solution :

When the similar figures is in the ratio of a : b, then volumes will be in the ratio of a³ : b³  of pyramid A and pyramid B.

The ratio of corresponding sides is 8 : 6, that is 

= 4 : 3

Volume of Pyramid A / Volume of pyramid B = (4/3)³

96/ Volume of pyramid B = 64/27

Volume of pyramid B = (96 x 27)/64

= 40.5 

So, volume of pyramid B is 40.5 cubic meters.

Example 7 :

A pyramid with a square base has a volume of 120 cubic meters and a height of 10 meters. Find the side length of the square base.

Solution :

Height = 10 m

Volume of pyramid = 120 cubic meters

(1/3) x base area x height = 120

1/3 x base area x 10 = 120

base area = (120 x 3)/10

= 36

Let x be the side length of the square.

x² = 36

x = 6

So, side length of the square base is 6 meters.

Example 8 :

A pyramid with a square base has a volume of 912 cubic feet and a height of 19 feet. Find the side length of the square base.

Solution :

volume of pyramid = 912 cubic feet

height = 19 feet

1/3 x base area x 19 = 912

base area = (912 x 3)/19

= 144

Let x be the side length of the square.

x² = 144

x = 12

So, side length of the square base is 12 meters.

Example 9 :

Describe and correct the error in finding the volume of the pyramid.

Solution :

To find volume of square base pyramid, we use the formula 

= 1/3 x base area x height

Since the base is in the shape of square, its area will be side x side

Side length of the square = 6 ft

Applying the side length, we get

= (1/3) x 6² x 5

= (1/3) x 36 x 5

= 60 cubic feet.