SOLVING GEOMETRIC PROBLEMS USING A SYSTEM OF EQUATIONS WORKSHEET

Problem 1 :

An equilateral triangle has sides of length (3x - y) cm, (x + 5) cm and (y + 3) cm. Find the length of each side.

Solution

Problem 2 :

The figure alongside is a rectangle. Find x and y.

Solution

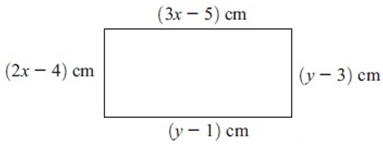
Problem 3 :

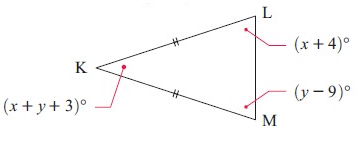
KLM is an isosceles triangle. Find x and y and hence find the measure of the angle at K.

Solution

Problem 4 :

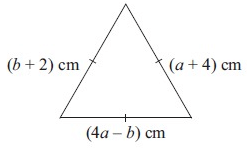
Given that the triangle alongside is equilateral, find a and b.

Solution

Problem 5 :

A rectangle has perimeter 32 cm. if 3 cm is taken from the length and added to the width, the rectangle becomes a square. Find the dimensions of the original rectangle.

Solution

Problem 6 :

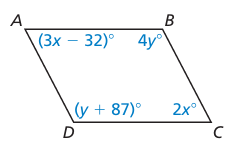
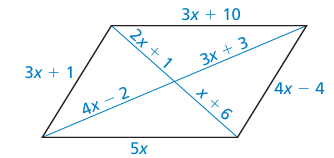
For what values of x and y is quadrilateral ABCD a parallelogram? Explain your reasoning.

Solution

Problem 7 :

What value of x makes the quadrilateral a parallelogram? Explain how you found your answer.

Solution

Problem 1 :

The diagonal of the TV screen is 82 cm, and the height is 40 cm. Calculate the width of the screen.

Solution

Problem 2 :

The aspect ratio of the rectangle and its diagonal is 9 : 12 : 15. Calculate the area of the rectangle if the length of the diagonal is 105 cm.

Solution

Problem 3 :

There is a rectangle with the length of 12 cm and diagonal 8 cm longer than the width. Calculate the area of the rectangle.

Solution

Problem 4 :

The length of the sides of the rectangular garden are in the ratio 1 : 2. The connection of the centers of the adjacent sides is 20 m long. Calculate the perimeter of the rectangle.

Solution

Problem 5 :

The dimension of the rectangular plot are (x + 1) m and (2x - y)m. The sum of x and y is 3 m and the perimeter of the plots is 36 m. Find the area of the diagonal of the plot.

Solution

Problem 6 :

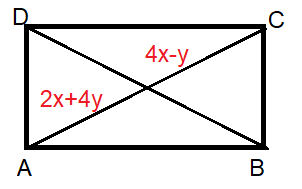
The diagonal of the rectangle given below is 36 m. Find the values of x and y.

Solution

Problem 7 :

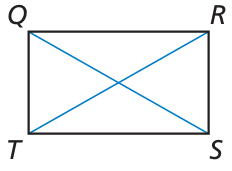
In rectangle QRST, QS = 5x − 31 and RT = 2x + 11. Find the lengths of the diagonals of QRST.

Solution

Problem 8 :

A rectangular carpet has area 120 square meters and perimeter 46 meters. The length of its diagonal is 

Solution

Problem 1 :

Two numbers have a sum of 200 and a difference of 37. Find the numbers.

Solution

Problem 2 :

The difference between two numbers is 84 and their sum is 278. What is the numbers?

Solution

Problem 3:     

One number exceeds another by 11. The sum of the two numbers is 5. What are the numbers?

Solution

Problem 4 :

The larger of two numbers is four times the smaller and their sum is 85. Find the two numbers.  

Solution

Problem 5 :

A wedding planner purchased both small and large lanterns for a wedding reception. The planner purchased a total of 40 lanterns for a purchase price of $1180. How many of each size lantern did the planner purchase?

Solution

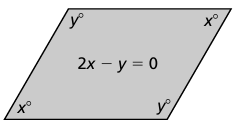
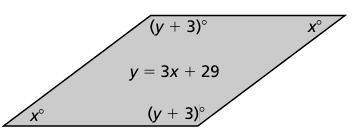
write an equation that represents the sum of the angle measures of the parallelogram and (b) use your equation and the equation shown to find the values of x and y.

Problem 6 :

Solution

Problem 7 :

Solution

Problem 1 :

y = -3x + 4

y = 4x - 10

Solution

Problem 2 :

y = -4x + 2

y = 6x - 8

Solution

Problem 3 :

x = - 2y

x - y = 9

Solution

Problem 4 :

y = 2x

-6x + 3y = 16

Solution

Problem 5 :

y = -3x

4x - 2y = -20

Solution

Problem 6 :

y = 3x - 4

4x + 3y = 1

Solution

Problem 7 :

y = x - 4

-4x - 6y = -16

Solution

Problem 8 :

x = 3y + 1

2x + 4y = 12

Solution

Problem 9 :

x = y - 4

-2x + 3y = 6

Solution

Problem 10 :

Next week your math teacher is giving a chapter test. The test will consist of 35 questions. Some problems are worth 2 points and some problems are worth 4 points. There are 20 questions worth 2 points. How many problems of 4 points are on the test?

Solution