SOLVING WORD PROBLEMS USING SYSTEMS OF EQUATIONS

Problem 1 :

Two numbers have a sum of 200 and a difference of 37. Find the numbers.

Solution :

Let x and y be two numbers.

x + y = 200 --- > (1)

x - y = 37 --- > (2)

From (2)

y = x - 37

Substitute y = x - 37 in (1)

x + (x - 37) = 200

x + x - 37 = 200

2x - 37 = 200

2x = 200 + 37

2x = 237

x = 237/2

x = 118 1/2

By applying x = 237/2 in (1)

237/2 + y = 200

y = 200 - 237/2

y = (400 - 237) / 2

y = 163/2

y = 81 1/2

So, two numbers are 118 1/2 and 81 1/2.

Problem 2 :

The difference between two numbers is 84 and their sum is 278. What is the numbers?

Solution :

x - y = 84 --- > (1)

x + y = 278 --- > (2)

From (1)

y = x - 84

Substitute y = x - 84 in (2)

x + (x - 84) = 278

x + x - 84 = 278

2x - 84 = 278

2x = 278 + 84

2x = 362

x = 362/2

x = 181

By applying x = 181 in (1)

181 - y = 84

-y = 84 - 181

-y = -97

y = 97

So, two numbers are 181 and 97. 

Problem 3:     

One number exceeds another by 11. The sum of the two numbers is 5. What are the numbers?

Solution :

x - y = 11 --- > (1)

x + y = 5 --- > (2)

From (1)

y = x - 11

Substitute y = x - 11 in (2)

x + (x - 11) = 5

x + x - 11 = 5

2x = 5 + 11

2x = 16

x = 8

By applying x = 8 in (2)

8 + y = 5

y = 5 - 8

y = -3

So, the numbers are 8 and -3.

Problem 4 :

The larger of two numbers is four times the smaller and their sum is 85. Find the two numbers.  

Solution :

Let x be the smaller number  and y be the larger number.

y = 4x --->(1)

x + y = 85 --->(2)

Substitute y = 4x in (2)

x + 4x = 85

5x = 85

x = 17

By applying x = 17 in (2)

17 + y = 85

y = 85 - 17

y = 68

So, two numbers are 17 and 68.

Problem 5 :

A wedding planner purchased both small and large lanterns for a wedding reception. The planner purchased a total of 40 lanterns for a purchase price of $1180. How many of each size lantern did the planner purchase?

Solution :

Let x be the number of small Lantern and y be the number of large Lantern.

x + y = 40 -----(1)

25x + 40y = 1180 -----(2)

From (1), y = 40 - x

Applying the value of y, we get

25x + 40(40 - x) = 1180

25x + 1600 - 40x = 1180

-15x = 1180 - 1600

-15x = -420

x = 420/15

x = 28

Applying x = 28, we get

y = 40 - 18

y = 12

So, number of small Lantern is 28 and number of large Lantern is 12.

write an equation that represents the sum of the angle measures of the parallelogram and (b) use your equation and the equation shown to find the values of x and y.

Problem 6 :

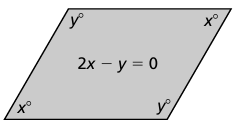
Solution :

x + y + x + y = 360

2x + 2y = 360

x + y = 180 -------(1)

2x - y = 0 -----(2)

y = 180 - x

Applying y = 180 - x in (2), we get

2x - (180 - x) = 0

2x - 180 + x = 0

3x = 180

x = 180/3

x = 60

Applying x = 60, we get

y = 180 - 60

y = 120

So, the value of x is 60 and value of y is 120.

Problem 7 :

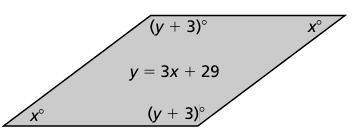
Solution :

x + y + 3 + x + y + 3 = 360

2x + 2y + 6 = 360

2x + 2y = 360 - 6

2x + 2y = 354

x + y = 177 -----(1)

y = 3x + 29 ------(2)

Applying the value of y in (1), we get

x + 3x + 29 = 177

4x = 177 - 29

4x = 148

x = 148/4

x = 37

Applying the value of x in (2), we get

y = 3(37) + 29

y = 111 + 29

y = 140

So, the value of x is 37 and y is 140.