PROBLEMS ON DIAGONALS OF  A RECTANGLE

A rectangle is also a parallelogram.

• In which the opposite sides are equal.
• Diagonal will have equal length and they will bisect each other.

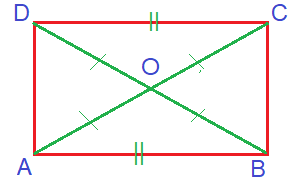
AO = CO

BO = DO

AC = BD

Problem 1 :

The diagonal of the TV screen is 82 cm, and the height is 40 cm. Calculate the width of the screen.

Solution :

The diagonal will divide the rectangle into two equal right triangles.

Width of the screen = length of the screen

(diagonal)² = (width)² + (length)²

82² = (width)² + (40)²

6724 = (width)² + 1600

Subtracting 1600 on both sides, we get

5124 = (width)²

Width = √5124

width = 71.58

Problem 2 :

The aspect ratio of the rectangle and its diagonal is 9 : 12 : 15. Calculate the area of the rectangle if the length of the diagonal is 105 cm.

Solution :

Length = 9x, width = 12x and diagonal = 15x

Length of the diagonal = 105 cm

15x = 105

x = 105/15

x = 7

Length = 9(7) ==> 63

width = 12(7) ==>  84

Area of rectangle = 63 (84)

= 5292 cm²

Problem 3 :

There is a rectangle with the length of 12 cm and diagonal 8 cm longer than the width. Calculate the area of the rectangle.

Solution :

Let x be the width of the rectangle.

diagonal = 8 + x, length = 12 cm

(8+x)² = x² + 12²

64 + 2x + x² = x² + 144

64 + 2x = 144

2x = 144 - 64

2x = 80

x = 40

Area of rectangle = 12x

= 12(40)

= 480 cm²

Problem 4 :

The length of the sides of the rectangular garden are in the ratio 1 : 2. The connection of the centers of the adjacent sides is 20 m long. Calculate the perimeter of the rectangle.

Solution :

Length = x and width = 2x

Distance between centers = 20 m

x² + (2x)² = 20²

x² + 4x² = 400

5x² = 400

x² = 80

x = 4√5

Perimeter of the rectangle = 2(x + 2x)

= 2(3x)

= 6(4√5)

= 24√5

Problem 5 :

The dimension of the rectangular plot are (x + 1) m and (2x - y)m. The sum of x and y is 3 m and the perimeter of the plots is 36 m. Find the area of the diagonal of the plot.

Solution :

Length = x +1, width = 2x - y

x + y = 3

y = 3 - x

Perimeter = 36 

2(x + 1 + 2x - y) = 36

2(3x - y + 1) = 36

(3x - y + 1) = 18

3x - (3 - x) + 1 = 18

3x - 3 + x = 17

4x = 20

x = 5

Then y = 3 - 5 ==> -2(doesn't mean the measure)

==> 5 + 1 ==> 6 m

Area of the plot = 6(8)

Area of plot = 48 square meter.

Problem 6 :

The diagonal of the rectangle given below is 36 m. Find the values of x and y.

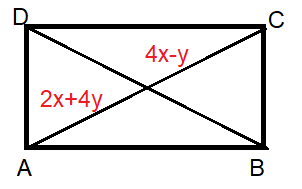
Solution :

Diagonals will bisect each other

So, 2x+4y = 4x-y

2x-4x + 4y + y = 0

-2x + 5y = 0  ---(1)

Length of diagonal = 36

2x + 4y + 4x - y = 36

6x + 3y = 36

Dividing by 3 on both sides.

2x + y = 12  ---(2)

(1) + (2)

6y = 12

y = 2

Applying y = 2 in (2), we get

2x + 2 = 12

2x = 10

x = 5