SOLVIGN GEOMETRIC PROBLEMS USIGN A SYSTEM OF EQUATIONS

Problem 1 :

An equilateral triangle has sides of length (3x - y) cm, (x + 5) cm and (y + 3) cm. Find the length of each side.

Solution :

Let the vertices of the given triangle be ABC.

AB = 3x - y, BC = x + 5 and CA = y + 3

Since it is equilateral triangle, all sides will be equal.

AB = BC, BC = CA and CA = AB

Equating AB and BC.

3x - y = x + 5

-y = x + 5 - 3x

-y = -2x + 5

y = 2x - 5 --- > (1)

Equating BC and CA.

x + 5 = y + 3

Applying the value of y, we get

x + 5 = 2x - 5 + 3

x - 2x = -5 - 5 + 3

-x = -7

x = 7

By applying x = 7 in (1)

y = 2(7) - 5

y = 14 - 5

y = 9

So, x = 7 and y = 9.

Problem 2 :

The figure alongside is a rectangle. Find x and y.

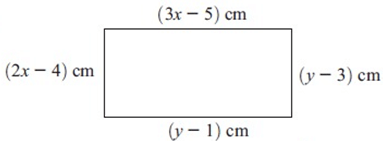
Solution :

Subtract (1) & (2)

3x - y - 2x + y = 4 - 1

x = 3

By applying x = 3 in (1)

3(3) - y = 4

9 - y = 4

-y = 4 - 9

-y = -5

y = 5

So, x = 3 and y = 5.

Problem 3 :

KLM is an isosceles triangle. Find x and y and hence find the measure of the angle at K.

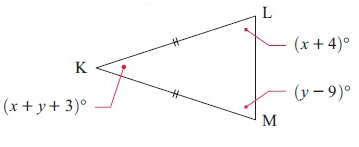
Solution :

 ∠K +  ∠L +  ∠M = 180°

x + y + 3 + x + 4 + y - 9 = 180°

2x + 2y = 180 + 9 - 7

2x + 2y = 182

Divide by 2 on both sides,

x + y = 91 --- > (1)

Since KL = KM,  ∠L =  ∠M

x + 4 = y - 9

y - x = 13 --- > (2)

Add (1) & (2), we get

x + y - x + y = 91 + 13

2y = 104

y = 52

By applying y = 52 in (1)

x + 52 = 91

x = 91 - 52

x = 39

Now,  ∠K = x + y + 3

 ∠K = 39 + 52 + 3

 ∠K = 94°

Problem 4:

Given that the triangle alongside is equilateral, find a and b.

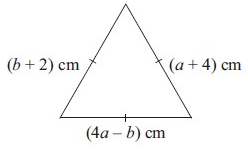
Solution :

Since the given triangle is equilateral triangle, the sides will be equal.

(b + 2) cm, (a + 4) cm and (4a - b) cm

The all sides of equilateral triangle are equal

Subtract (1) & (2)

a - b - 2a + b = -2 - 1

-a = -3

a = 3

By applying a = 3 in (1)

3 - b = -2

-b = -2 - 3

-b = -5

b = 5

So, a = 3 and b = 5. 

Problem 5 :

A rectangle has perimeter 32 cm. if 3 cm is taken from the length and added to the width, the rectangle becomes a square. Find the dimensions of the original rectangle.

Solution :

Let length and width be L and W respectively.

2L + 2W = 32 --- > (1)

L - 3 = W + 3

L = W + 6

Substitute L = W + 6 in (1)

2(W + 6) + 2W = 32

2W + 12 + 2W = 32

4W + 12 = 32

4W = 32 - 12

4W = 20

W = 20/4

W = 5

By applying W = 5 in L = W + 6

L = 5 + 6

L = 11

So, original dimension of rectangle, length is 11 cm and width is 5 cm.