SOLVING EXPONENTIAL EQUATIONS WITH LOGARITHMS WORKSHEET

Solve the following equations.

Problem 1 :

3^x - 2 = 12

Solution

Problem 2 :

3^1-x = 2

Solution

Problem 3 :

4^x = 5^x+1

Solution

Problem 4 :

6^1-x = 10^x

Solution

Problem 5 :

3^2x+1 = 2^x-2

Solution

Problem 6 :

10/(1+ e^-x) = 2

Solution

Problem 7 :

5^2x - 5^x - 12 = 0

Solution

Problem 8 :

e^2x - 2e^x = 15

Solution

Problem 9 :

You scan a photo into a computer at four times its original size. You continue to increase its size repeatedly by 100% using the computer. The new size of the photo y in comparison to its original size after x enlargements on the computer is represented by

y = 2^{x + 2}

How many times must the photo be enlarged on the computer so the new photo is 32 times the original size?

Problem 10 :

A bacterial culture quadruples in size every hour. You begin observing the number of bacteria 3 hours after the culture is prepared. The amount y of bacteria x hours after the culture is prepared is represented by

y = 192(4^{x - 3})

When will there be 196,608 bacteria?

Problem 11 :

Solve the equation by using the Property of Equality for Exponential Equations.

30 ⋅ 5^{x + 3} = 150

Find the value of y.

Solution

Problem 13 :

Describe the similarities and difference between in solving the equations 

4^{5x - 2} = 16 and log₄(10x + 6) = 1

Then solve the each equation

Solution

Problem 14 :

For a sound with intensity I (in watts per square meter) the loudness L(I) of the sound (in decibels) is given by the function

L(I) = 10 log (I/I₀)

Where I0 is the intensity of barely audible sound (about 10^-12 watts per square meter) An artist in a recording studio turns up the volume of a track so that the intensity of the sound doubles. By how many decibels does the loudness increase ?

Solution

Problem 15 :

The length ℓ (in centimeters) of a scalloped hammerhead shark can be modeled by the function

ℓ = 266 − 219e^−0.05t

where t is the age (in years) of the shark. How old is a shark that is 175 centimeters long?

Use the One-to-One Property to solve the equation for x.

Problem 1 :

log₂(x + 1) = log₂ 4

Solution

Problem 2 :

log₂(x - 3) = log₂ 9

Solution

Problem 3 :

log(2x + 1) = log 15

Solution

Problem 4 :

log(5x + 3) = log 12

Solution

Problem 5 :

ln(x + 2) = ln 6

Solution

Problem 6 :

ln(x - 4) = ln 2

Solution

Problem 7 :

ln(x² - 2) = ln 23

Solution

Problem 8 :

ln(x² - x) = ln 6

Solution

Problem 9 :

A population of 30 mice is expected to double each year. The number p of mice in the population each year is given by p = 30(2ⁿ). In how many years will there be 960 mice in the population?

Solution

Problem 10 :

Approximate the solution of each equation using the graph

1 − 5^{5 − x} = −9

Solution

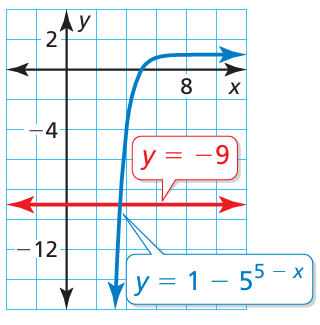
Problem 11 :

Approximate the solution of each equation using the graph

log₂5x = 2

Solution

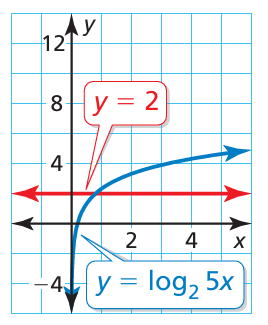
Problem 12 :

The apparent magnitude of a star is a measure of the brightness of the star as it appears to observers on Earth. The apparent magnitude M of the dimmest star that can be seen with a telescope is

M = 5 log D + 2

where D is the diameter (in millimeters) of the telescope’s objective lens. What is the diameter of the objective lens of a telescope that can reveal stars with a magnitude of 12?

Solution

Problem 13 :

A biologist can estimate the age of an African elephant by measuring the length of its footprint and using the equation

ℓ = 45 − 25.7e^−0.09a

where ℓ is the length (in centimeters) of the footprint and a is the age (in years).

a. Rewrite the equation, solving for a in terms of ℓ.

b. Use the equation in part (a) to find the ages of the elephants whose footprints are shown.

Solution