SOLVING EXPONENTIAL EQUATIONS WITH LOARITHMS

To solve logarithmic equation, first we should know how to convert the logarithmic form to exponential form.

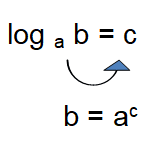
Some of the rules in logarithm :

log m + log n = log (m x n)

log m - log n = log (m / n)

log mⁿ = n log m

log _a a = 1

If we don't have any base for logarithm, we will consider its base as 10.

Solve the following equations.

Problem 1 :

3^x - 2 = 12

Solution :

3^x - 2 = 12

3^x = 12 + 2

3^x = 14

We cannot write 14 as multiple of 3. So, take logarithms of both sides.

log 3^x = log 14

x log 3 = log 14

x = log 14 / log 3

x = 1.1461/0.4771

x = 2.402

Problem 2 :

3^1-x = 2

Solution :

3^1-x = 2

(1 - x) log 3 = log 2

log 3 - x log 3 = log 2

log 3 - log 2 = x log 3

0.4771 - 0.3030 = 0.4771 x

0.1761 = 0.4771 x

x = 0.1761 / 0.4771

x = 0.3691

Problem 3 :

4^x = 5^x+1

Solution :

4^x = 5^x+1

log 4^x = log 5^x+1

 x log 4 = (x + 1) log 5

x log 4 = x log 5 + log 5

x(log 4 - log 5) = log 5

x(0.6020 - 0.6989) = 0.6989

-0.0969 x = 0.6989

x = 0.6989 / -0.0969

x = -7.213

Problem 4 :

6^1-x = 10^x

Solution :

6^1-x = 10^x

log 6^1-x = log 10^x

(1 - x) log 6 = x log 10

log 6 - x log 6 = x log 10

log 6 = x log 10 + x log 6

log 6 = x(log 10 + log 6)

0.7786 = x (1 + 0.7786)

0.7786 = 1.7786x

x = 0.7786 / 1.7786

x = 0.438

Problem 5 :

3^2x+1 = 2^x-2

Solution :

3^2x+1 = 2^x-2

log 3^2x+1 = log 2^x-2

(2x + 1) log 3 = (x - 2) log 2

2x log 3 + log 3 = x log 2 - 2 log 2

2x log 3 - x log 2 = -2 log 2 - log 3

x(2 log 3 - log 2) = -2 log 2 - log 3

x[(2 × 0.4771) - 0.3010] = -2(0.3010) - 0.4771

0.9542 - 0.3010 x = - 0.602 - 0.4771

0.6532 x = - 1.0791

x = -1.0791 / 0.6532

x = -1.652

Problem 6 :

10/(1+ e^-x) = 2

Solution :

10 /(1+ e^-x) = 2

10 = 2(1+ e^-x)

10 = 2 + 2e^-x

2e^-x = 10 - 2

2e^-x = 8

e^-x = 8/2

e^-x = 4

-x = ln 4

x = -ln4 

Problem 7 :

5^2x - 5^x - 12 = 0

Solution :

5^2x - 5^x - 12 = 0

t = 5^x

Rewrite the equation

t² - t - 12 = 0

(t - 4) (t + 3) = 0

t = 4 or t = -3

t = 5⁴

So, x = log₅ 4

Problem 8 :

e^2x - 2e^x = 15

Solution :

e^2x - 2e^x = 15

 t = e^x

Rewrite the equation

t² - 2t - 15 = 0

(t - 5) (t + 3) = 0

t = 5 or t = -3

t = 5

So, x = ln 5