PROPERTIES OF PARALLELOGRAM

Problem 1 :

Find each measure in parallelogram

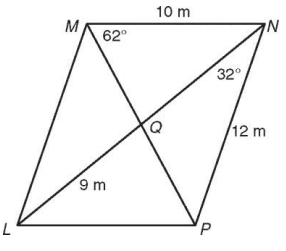
Find, 

1)  ML    2)  LP   3)  ∠LPM   4)  ∠MLN    5)  LN    6)  QN

Solution :

Since it is parallelogram, the opposite sides are parallel and equal ML = PN and LP = MN

1)  ML = 12 m

2)  LP = 10 m

3)  MN and LP are parallel, MP is a transversal. 

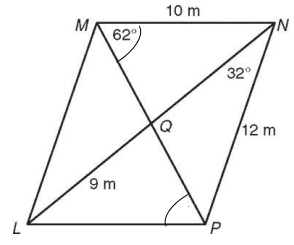
∠PMN = ∠LPM = 62° (Alternate interior angles)

4)  ∠MLN

LM parallel to PN, then 

∠MLN = ∠LNP = 32° (Alternate interior angles)

5)  LN :

Since the diagonal will bisect each other, LP = NQ

LN = 2LP

LN = 2(9) ==> 18

6)  QN = 9 m

Problem 2 :

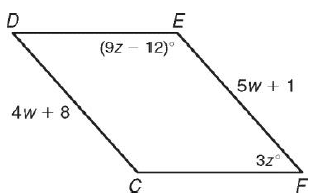
CDEF is a parallelogram. Find each measure.

(i)  CD   (ii)  EF     (iii)  ∠E     (iv)  ∠F

Solution :

In parallelogram opposite sides will be equal.

CD = EF

Sum of consecutive interior angles = 180.

9z - 12 + 3z = 180

12z - 12 = 180

12z = 192

z = 192/12

z = 16

Problem 3 :

Quadrilateral RSTU is a parallelogram. Find the values of x, y, a, and b.

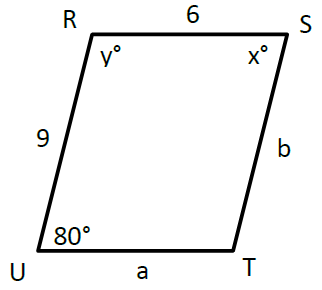
Solution :

x = 80° 

x + y = 180 (Consecutive interior angles)

80 + y = 180

y = 180 - 80

y = 100

a = 6 and b = 9

Problem 4 :

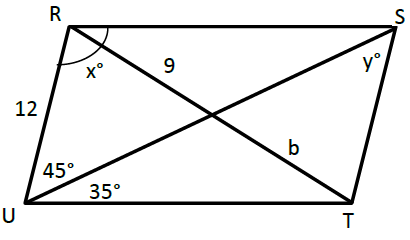
Solution :

In triangle RUS.

∠URS + ∠RSU + ∠SUR = 180

∠RSU = 35 (Alternate interior angles)

x + 35 + 45 = 180

x + 80 = 180

x = 180 - 80

x = 100

y = 45 (Alternate interior)

Diagonal will bisect each other. So, b = 9.

Problem 5 :

Find the missing measurements of parallelogram.

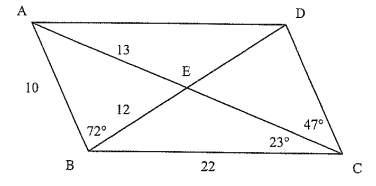
Find the measures of 

Solution :

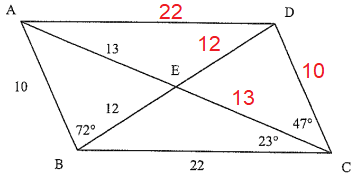
1) CD = 10 (Opposite sides)

2)  AC = 13 + 13 ==> 26

3)  CE = 13

4)  DA = 22 (Opposite sides)

5)  DB = 12 + 12 ==> 24

6)  DE = 12

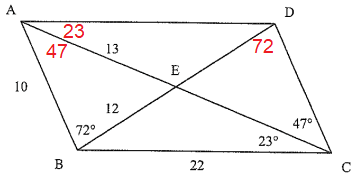
7)  In triangle ABC,

∠EBC = x

∠EAB + ∠ABE + ∠EBC + ∠BCE = 180

47 + 72 + x + 23 = 180

142 + x = 180

x = 180 - 142

x = 38

∠ABC = 72 + 38 ==>  110

8) ∠BCD = 23 + 47 ==>  70

9) ∠BAD = 23 + 47 ==>  70

10) ∠DAE = 23

11) ∠BEC :

In triangle BEC,

38 + 23 + ∠BEC = 180

∠BEC = 180 - 61

∠BEC = 119

12)  ∠BCE = 23

13) ∠ADC :

∠ABC = ∠ADC  =  110 (opposite angles)

14)  ∠CDE = 72 (Alternate angles)

15)  ∠EAB = 47

16)  ∠CED :

∠CED = 180 - (47 + 72)

∠CED = 180 - 119

∠CED = 61

17)  ∠EDA = 38 (alternate interior angles)

18)  ∠AEB = 61

19)  ∠DEA = 119

Problem 6 :

In the figure given below, ABCD is a parallelogram. Find the values of x, y, z and p.

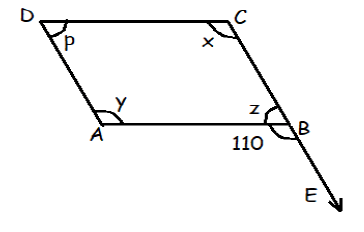
Solution :

110 + z = 180

z = 180 - 110

z = 70

In parallelogram sum of consecutive angles = 180

y + z = 180

y + 70 = 180

y = 110

Opposite angles are equal,

So, x = 110 and p = 70

Problem 7 :

State whether each statement is always, sometimes, or never true for a parallelogram. Explain your reasoning.

a. The opposite sides are congruent.

b. All four sides are congruent.

c. The diagonals are congruent.

d. The opposite angles are congruent.

e. The adjacent angles are congruent.

f. The adjacent angles are complementary

Solution :

a. In parallelogram, always opposite sides will be congruent.

b. In parallelogram, sometimes all four sides will be congruent. Then it is rhombus.

c. In parallelogram, sometimes the diagonals are congruent.

d. The opposite angles are congruent always.

e. Sometimes the adjacent angles are congruent. When adjacent angles are equal, its measure must be 90 degree, then that shape is known as rectangle.

f. The adjacent angles will never be complementary, because the sum of adjacent angles must be add up to 180 degree.

Related Pages

• Find missing angles in parallelogram
• Find missing angles of parallelogram worksheet
• Length of diagonal of parallelogram
• Length of diagonal of parallelogram worksheet
• Properties of parallelogram worksheet