HOW TO FIND THE LENGTH OF DIAGONAL OF A PARALLELOGRAM

Definition of parallelogram :

A parallelogram is a quadrilateral which has opposite sides parallel.

Properties of parallelogram :

• Opposite sides are equal in length
• Opposite angles are equal in size.
• Diagonals bisect each other.
• Consecutive interior angles add upto 180.

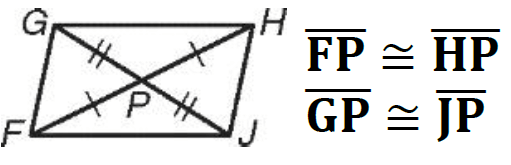
Problem 1 :

For the parallelogram given below, solve for m and n.

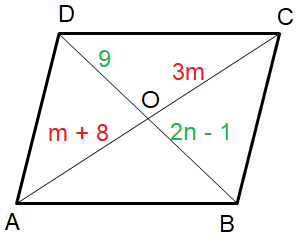
Solution :

Since the given shape is a parallelogram, the diagonals will bisect each other.

Problem 2 :

For the parallelogram given below, solve for j and k.

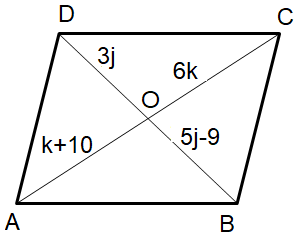
Solution :

Problem 3 :

In parallelogram PQRS, solve for x and y.

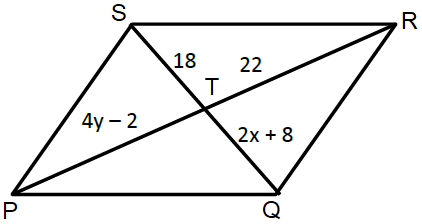
Solution :

Problem 4 :

Solve the n in the following parallelogram ABCD. Find length of the diagonal BD.

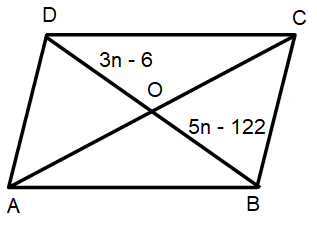
Solution :

Diagonals will bisect each other.

3n - 6 = 5n - 122

3n - 5n = -122 + 6

-2n = -116

Dividing by 2 on both sides.

n = 116/2

n = 58

Length of BD = 3n - 6 + 5n - 122

= 8n - 128

= 8(58) - 128

= 464 - 128

= 336

So, length of the diagonal BD is 336.

Problem 5 :

Length of the longer diagonal in the parallelogram FAST.

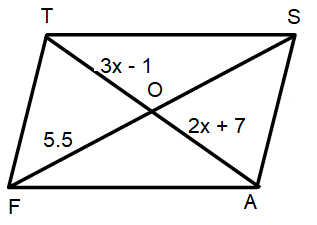
Solution :

FO = 5.5, then FS = 5.5(2) ==>  11

TO = 3x - 1, OA = 2x + 7

3x - 1 = 2x + 7

3x - 2x = 7 + 1

x = 8

Length of diagonal TA = 3x - 1 + 2x + 7

= 5x + 6

= 5(8) + 6

= 40 + 6

= 46

So, length of the longer diagonal is 46.