LENGTH OF DIAGONAL OF A PARALLELOGRAM WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
For the parallelogram given below, solve for m and n.
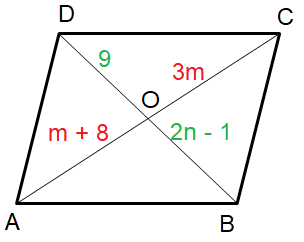
Problem 2 :
For the parallelogram given below, solve for j and k.
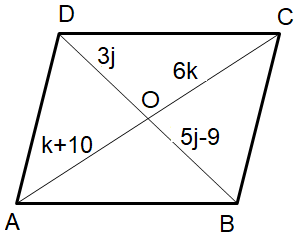
Problem 3 :
In parallelogram PQRS, solve for x and y.
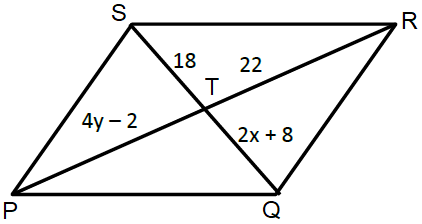
Problem 4 :
Solve the n in the following parallelogram ABCD. Find length of the diagonal BD.
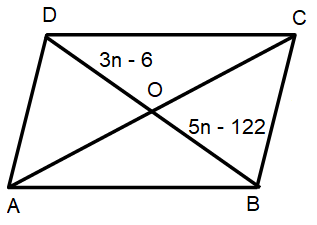
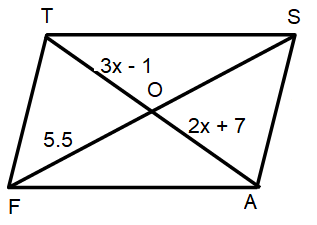
Problem 5 :
Length of the longer diagonal in the parallelogram FAST.
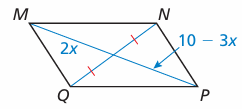
Problem 6 :
For what value of x is quadrilateral MNPQ a parallelogram? Explain your reasoning
Problem 7 :
find the value of x that makes the quadrilateral a parallelogram.
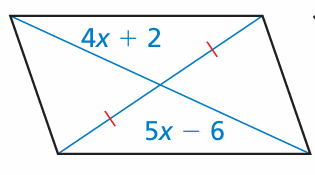
Problem 8 :
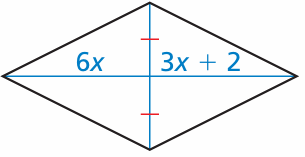
Problem 9 :
What value of x makes the quadrilateral a parallelogram? Explain how you found your answer.
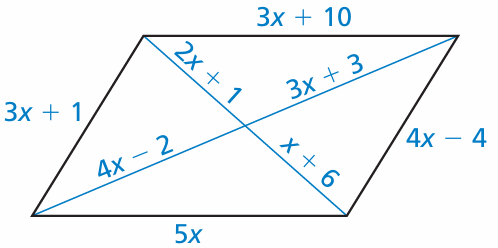
Problem 10 :
Find the value of each variable in the parallelogram.
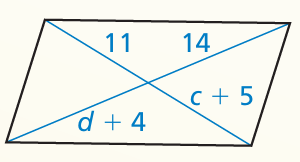
Problem 11 :
Find the coordinates of the intersection of the diagonals of ▱QRST with vertices Q(−8, 1), R(2, 1), S(4, −3), and T(−6, −3).
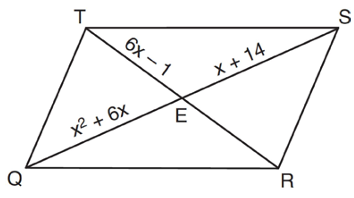
Problem 12 :
As shown in the diagram below, the diagonals of parallelogram QRST intersect at E. If QE = x2 + 6x, SE = x + 14, and TE = 6x − 1, determine TE algebraically
Answer Key
1) m = 4, n = 5
2) k = 2 and j = 4.5
3) x = 5 and y = 6
4) n = 58, length of the diagonal BD is 336.
5) length of the longer diagonal is 46.
6) the value of x is 2.
7) the value of x is 8
8) the value of x is 2/3.
9) x = 5
10) c = 6 and d = 10
11) (-2, -1)
12) the length TE is 11.
Problem 1 :
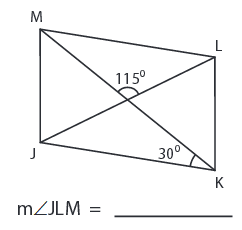
Problem 2 :
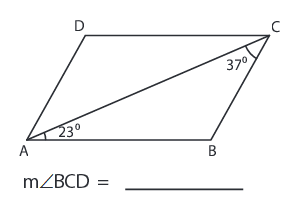
Problem 3 :
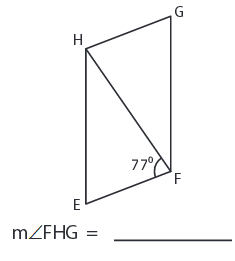
Problem 4 :
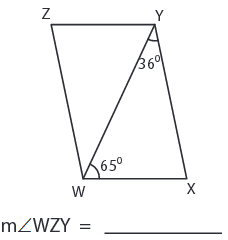
Problem 5 :
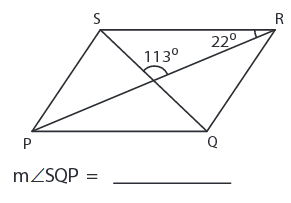
Problem 6:
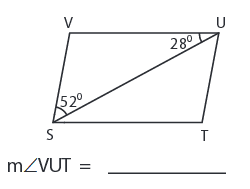
Problem 6 :
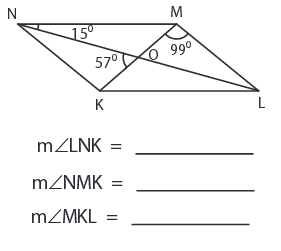
Problem 7 :
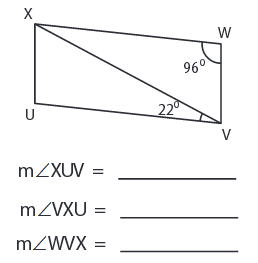
Problem 8 :
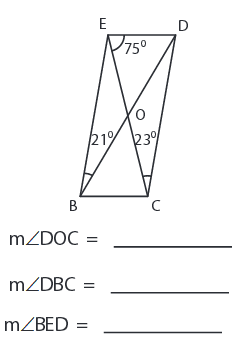
Problem 9 :
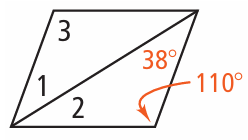
Problem 10 :
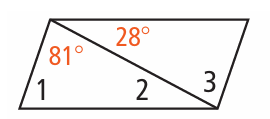
Problem 11 :
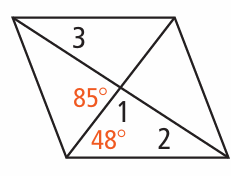
Problem 12 :
ABCD is a parallelogram in which ∠DAB = 70o and ∠CBD = 55o. Find ∠CDB and ∠ADB.
Problem 13 :
In a parallelogram ABCD, ∠A = (2x + 10)o and ∠C = (3x – 20)o. Find the value of x.
Problem 14 :
The sum of the two opposite angles of a parallelogram is 150o. Find all the angles of the parallelogram.
Problem 15 :
If the angles of a quadrilateral are (x – 20)o, (x + 20)o, (x – 15)o and (x + 15)o, find x and the angles of the quadrilateral
Answer Key
1) ∠JLM = 35°
2) ∠BCD = 60°
3) ∠FHG = 77°
4) ∠WZY = 79°
5) ∠SQP = 45°
6) ∠VUT = 80°
7) ∠LNK = 24°, ∠OMN = 42°, ∠MKL = ∠NMK = 42°
8) ∠WVX = ∠VXU = 62°
9) ∠DOC = 136°, ∠DBC = 61°, ∠BED = 98°
10) ∠1 = 38, ∠2 = 32, ∠3 = 110
11) ∠1 = 71, ∠2 = 28, ∠3 = 81
12) ∠1 = 95, ∠2 = 37
13)
∠CDB = 55
∠ADB = 55 (alternate interior angles)
14) the value of x is 30
15) the all four angles are 75, 75, 105 and 105.
16) the all four angles are 70, 110, 65 and 105.
Problem 1 :
Side length = 2 yd
Diagonal = _______
Problem 2 :
Side length = 53 ft
Diagonal = _______
Problem 3 :
Side length = 17.3 in
Diagonal = _______
Problem 4 :
Side length = 95 yd
Diagonal = _______
Find the length of the diagonal of each square. Round your answer to the nearest tenth.
Problem 5 :
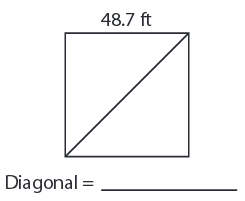
Problem 6 :
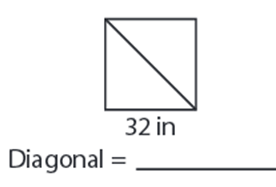
Problem 7:
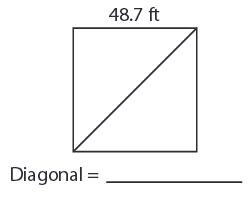
Problem 8 :
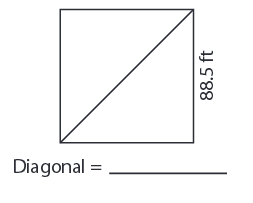
Problem 9 :
The side length of a square is 22 yards. What is the length of the diagonal?
Problem 10 :
The diagonals of two squares are in the ratio of 2 : 5. Find the ratio of their areas.
Problem 11 :
If length of diagonal of a square is 20 cm, then its perimeter is ________
Problem 12 :
A rectangular carpet has area 120 square meters and perimeter 46 meters. The length of its diagonal is ___________ .
Problem 13 :
If diagonal of a rectangle is thrice its smaller side, then find the ratio of its length and width.
Problem 14 :
If diagonal of one square is double the diagonal of another square, then find the ratio of their areas.
Problem 15 :
The length of the diagonal of a square is 50. Find the perimeter of a square.
Answer Key
1) Diagonal = 2.8 yd
2) Diagonal = 75 ft
3) Diagonal = 24.5 in
4) Diagonal = 134.4 yd
5) Diagonal = 68.9 ft
6) Diagonal = 45.3 in
7) Diagonal = 99 yd
8) Diagonal = 125.2 ft
9) Diagonal = 31.1 yards
10) the ratio between the areas is 4 : 2
11) the perimeter of the square is 40√2 cm.
12) the length of the diagonal is 17 cm.
13) the required ratio is 2√2 : 2.
14) 4 : 1
15) 100√2 cm
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling