HOW TO FIND THE ANGLES OF A PARALLELOGRAM

Find the measures of the indicated angles in each parallelogram.

Problem 1 :

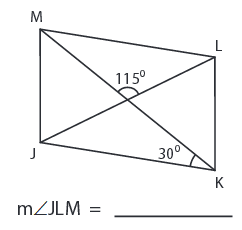
Solution :

The sum of the interior angles of a triangle is 180°.

∠KML = ∠MKJ = 30°

∠KML + ∠JLM + 115° = 180°

∠JLM  + 30° + 115° = 180°

∠JLM = 180° - 115° - 30°

∠JLM = 35°

Problem 2 :

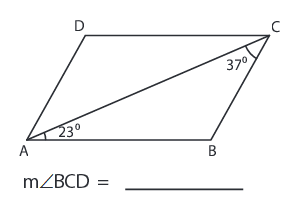
Solution :

DC II AB

 ∠DCA = ∠BAC = 23°

∠BCD = ∠ACB + ∠DCA

∠BCD = 23° + 37°

∠BCD = 60°

Problem 3 :

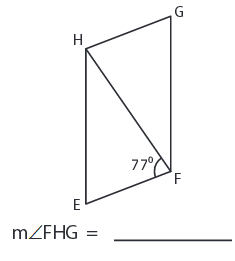
Solution :

The opposite angles are equal in a parallelogram.

∠FHG = ∠HFE = 77°

So, ∠FHG = 77°

Problem 4 :

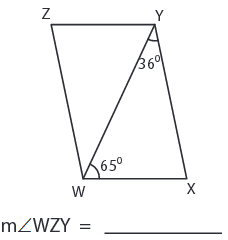
Solution :

The opposite angles are equal in a parallelogram.

∠WZY = ∠WXY

The sum of the interior angles of a triangle is 180°.

∠WXY = 180° - ∠XWY - ∠WYX

∠WZY = = 180° - 65° - 36°

∠WZY = = 79°

∠WZY = 79°

Problem 5:

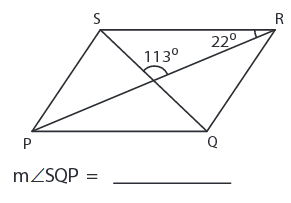
Solution :

The sum of the interior angles of a triangle is 180°.

∠SQP = 180° - (113 + 22)

∠SQP = 180° - 135°

∠SQP = 45°

Problem 6:

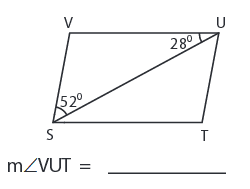
Solution :

∠VUT = ∠SUV + ∠SUT

∠VUT = 28° + 52°

∠VUT = 80°

Problem 6 :

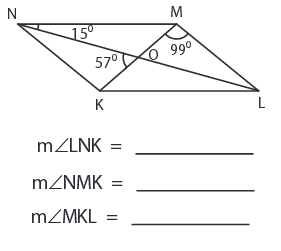
Solution :

In MNKL, ML II NK

So, ∠LNK = ∠NLM

∠MOL = ∠KON = 57° (vertical angles are equal)

∠LNK = 180° - ∠OML - ∠MOL

∠LNK = 180° - 99° - 57°

∠LNK = 24°

In ∆OMN,

∠NOK = ∠LNM + ∠OMN

∠OMN = ∠NOK - ∠LNM

∠OMN = 57° - 15°

∠OMN = 42°

The outside angle of a triangle is equal to the sum of two interior angles that are not adjacent to it.

NM II KL,

So, ∠MKL = ∠NMK = 42°

Problem 7 :

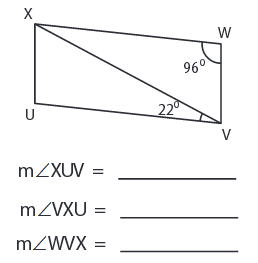
Solution :

∠XUV = ∠XWV = 96°

∠VXU = 180° - ∠XWV - ∠XVU

∠VXU = 180° - 96° - 22°

∠VXU = 62°

∠WVX = ∠VXU = 62°

Problem 8 :

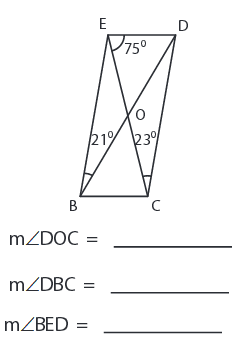
Solution :

BE II DC,

∠EBD = ∠BDC = 21°

∠DOC = 180° - (∠BDC + ∠DCE)

∠DOC = 180° - (21 + 23)

∠DOC = 180° - 44°

∠DOC = 136°

ED II BC,

∠DEC = ∠ECB = 75°

∠DBC = ∠DOC - ∠ECB

∠DBC = 136° - 75°

∠DBC = 61°

∠ECD = ∠BEC = 23°

∠BED = ∠BEC + ∠DEC

∠BED = 23° + 75°

∠BED = 98°

Find the measures of the numbered angles for each parallelogram.

Problem 9 :

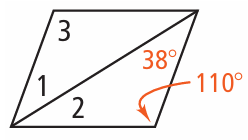
Solution :

Opposite angels will be equal.

∠3 = 110

Adjacent angles are co-interior angles.

∠1 + ∠2 = 180 - 110

∠1 + ∠2 = 70

∠1 = 38

38 + ∠2 = 70

∠2 = 70 - 38

∠2 = 32

Problem 10 :

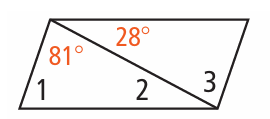
Solution :

∠2 = 28

∠3 = 81

∠1 + 81 + 28 = 180

∠1 + 109 = 180

= 180 - 109

∠1 = 71

Problem 11 :

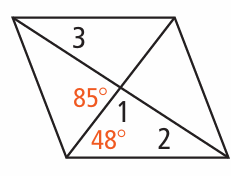
Solution :

∠3 = ∠2 (Alternate interior angles)

∠1 + 85 = 180 (linear pair)

∠1 = 180 - 85

∠1 = 95

Sum of interior angles of triangle = 180

95 + 48 + ∠2 = 180

143 + ∠2 = 180

∠2 = 180 - 143

∠2 = 37

Problem 12 :

ABCD is a parallelogram in which ∠DAB = 70^o and ∠CBD = 55^o. Find ∠CDB and ∠ADB.

Solution :

In parallelogram, opposite angels will be equal.

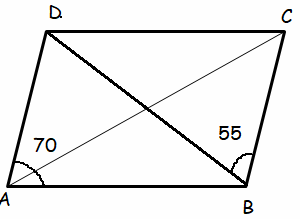
In triangle CDB,

∠CDB + ∠CBD + ∠DCB = 180

∠DCB = ∠DCB

∠CDB + 55 + 70 = 180

∠CDB + 125 = 180

∠CDB = 180 - 125

∠CDB = 55

∠ADB = 55 (alternate interior angles)

Problem 13 :

In a parallelogram ABCD, ∠A = (2x + 10)^o and ∠C = (3x – 20)^o. Find the value of x.

Solution :

In parallelogram ABCD, ∠A and ∠C are opposite angles and they must be equal.

2x + 10 = 3x - 20

2x - 3x = -20 - 10

-x = -30

x = 30

So, the value of x is 30

Problem 14 :

The sum of the two opposite angles of a parallelogram is 150^o. Find all the angles of the parallelogram.

Solution :

Opposite angles will be equal in parallelogram and sum of adjacent angles will be add up to 180 degree.

One angle measure = 150/2

= 75

75 + adjacent angle = 180

adjacent angle = 180 - 75

= 105

So, the all four angles are 75, 75, 105 and 105.

Problem 15 :

If the angles of a quadrilateral are (x – 20)^o, (x + 20)^o, (x – 15)^o and (x + 15)^o, find x and the angles of the quadrilateral

Solution :

Sum of interior angles of quadrilateral = 360

(x – 20) + (x + 20) + (x – 15) + (x + 15) = 360

4x = 360

x = 360/4

x = 90

Applying the value of x, we get

x - 20 ==> 90 - 20 ==> 70

x + 20 ==> 90 + 20 ==> 110

x - 15 ==> 90 - 15 ==> 65

x + 15 ==> 90 + 15 ==> 105

So, the all four angles are 70, 110, 65 and 105.