HOW TO FIND THE DIAGONAL OF A SQUARE

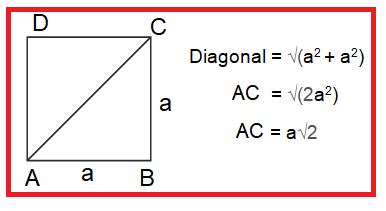
A square is a four-sided polygon which has it's all sides equal in length and the measure of the angles are 90 degrees.

The diagonal will divide the square into two right triangles.

Find the length of the diagonal of each square. Round your answer to the nearest tenth.

Problem 1 :

Side length = 2 yd

Diagonal = _______

Solution :

Length of the Diagonal = √2 ∙ a

= 1.414 × 2

Diagonal = 2.8 yd

Problem 2 :

Side length = 53 ft

Diagonal = _______

Solution :

Length of the Diagonal = √2 ∙ a

= 1.414 × 53

Diagonal = 75 ft

Problem 3 :

Side length = 17.3 in

Diagonal = _______

Solution :

Length of the Diagonal = √2 ∙ a

= 1.414 × 17.3

Diagonal = 24.5 in

Problem 4 :

Side length = 95 yd

Diagonal = _______

Solution :

Length of the Diagonal = √2 ∙ a

= 1.414 × 95

Diagonal = 134.4 yd

Find the length of the diagonal of each square. Round your answer to the nearest tenth.

Problem 5 :

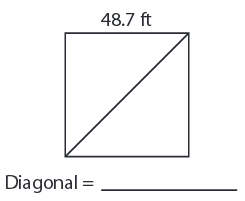
Solution :

Side length = 48.7 ft

Length of the Diagonal = √2 ∙ a

= 1.414 × 48.7

Diagonal = 68.9 ft

Problem 6 :

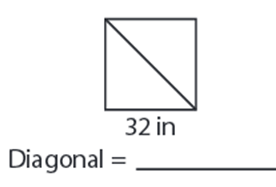
Solution :

Given, side length = 32 in

Length of the Diagonal = √2 ∙ a

= 1.414 × 32

Diagonal = 45.3 in

Problem 7:

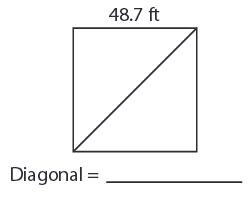
Solution :

Side length = 70 yd

Length of the Diagonal = √2 ∙ a

= 1.414 × 70

Diagonal = 99 yd

Problem 8 :

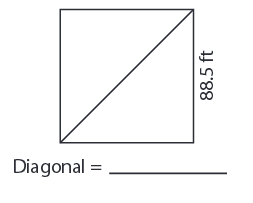
Solution :

Side length = 88.5 ft

Length of the Diagonal = √2 ∙ a

= 1.414 × 88.5

Diagonal = 125.2 ft

Problem 9 :

The side length of a square is 22 yards. What is the length of the diagonal?

Solution :

Side length = 22 yards

Length of the Diagonal = √2 ∙ a

= 1.414 × 22

Diagonal = 31.1 yards

Problem 10 :

The diagonals of two squares are in the ratio of 2 : 5. Find the ratio of their areas.

Solution :

Let 2x and 5x be length of diagonals.

Length of diagonal = √2 ∙ a

Where a is the side length of the square.

2x = √2 ∙ a

a = 2x/√2

5x = √2 ∙ a

a = 5x/√2

Ratio between the area of two square :

(2x/√2)² : (5x/√2)²

4x²/2 : 25x²/2 

4 : 25

So, the ratio between the areas is 4 : 25.

Problem 11 :

If length of diagonal of a square is 20 cm, then its perimeter is ________

Solution :

Length of diagonal = √2 ∙ a

Where a is the side length of the square.

20 = √2 ∙ a

a = 20/√2

= 20(√2)/2

= 10√2

So, the side length of the square is 10√2 cm

Perimeter = 4(side length)

= 4(10√2)

= 40√2 cm

So, the perimeter of the square is 40√2 cm.

Problem 12 :

 A rectangular carpet has area 120 square meters and perimeter 46 meters. The length of its diagonal is ___________ .

Solution :

Let x and y be the length and width of rectangle.

xy = 120 -----(1)

2(x + y) = 46

x + y = 46/2

x + y = 23

y = 23 - x

Applying the value of y = 23 - x i n(2)

x(23 - x) = 120

23x - x² = 120

x² - 23 x = -120

x² - 23 x + 120 = 0

(x - 15)(x - 8) = 0

x = 15 and x = 8

When x = 15, y = 23 - 15 ==> 8

When x = 8, y = 23 - 8 ==> 15

The length of diagonal :

d² = x² + y²

= 15² + 8²

= 225 + 64

= 289

d = √289

d = 17 cm

So, the length of the diagonal is 17 cm.

Problem 13 :

If diagonal of a rectangle is thrice its smaller side, then find the ratio of its length and width.

Solution :

Let x be the width of the rectangle then length of the diagonal is 3x.

(Diagonal)² = length² + width²

(3x)² = length² + x²

9x² - x² = length²

8x² = length²

length = √8x²

= 2x√2

Ratio between length and width of the rectangle = 2x√2 : x

= 2√2 : 2

so, the required ratio is 2√2 : 2.

Problem 14 :

If diagonal of one square is double the diagonal of another square, then find the ratio of their areas.

Solution :

Let d₁ and d₂ be diagonals of two squares.

d₁ = 2d₂

Area of square from diagonal = (diagonal)²/2

Area of first square = (d₁)²/2

= (2d₂)²/2

= 4d_2²/2

= 2d_2²

Area of second square = (d₂)²/2

Ratio between area of squares = 2d_{2² : (d2)²/2}

= 4 : 1

Problem 15 :

The length of the diagonal of a square is 50. Find the perimeter of a square. 

Solution :

Length of diagonal = √2 ∙ a

50 = √2 ∙ a

a = 50/√2

= 50(√2)/2

 = 25√2

Perimeter of the square = 4(side length)

= 4(25√2)

= 100√2 cm