PRACTICE QUESTIONS ON SIMPLIFYING RADICALS

Simplifying Radicals By Finding Perfect Square Factors

Questions :

1)  √75      Solution

2)  √16     Solution

3)  √36       Solution

4)  √64     Solution

5)  √80       Solution

6)  √30       Solution

7)  √8      Solution

8)  √18         Solution

9)  √32        Solution

10)  √12        Solution

11)  √108      Solution

12)  √125         Solution

13)  √50      Solution

14)  √175     Solution

Problem 15 :

The circumference C of the art room in a mansion is approximated by the formula C ≈ 2π √[a² + b² /2]. Approximate the circumference of the room.

Solution

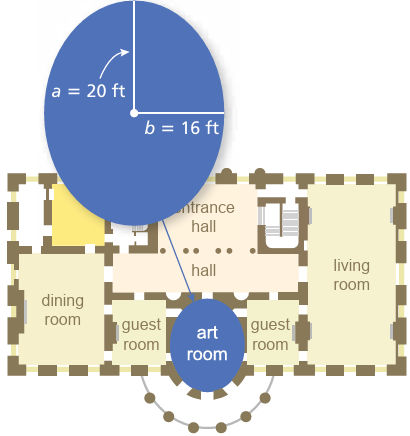
Problem 16 :

26 a perfect square?

Solution

Problem 17 :

Can the square of an integer be a negative number? Explain.

Solution

Problem 18 :

Does √256 represent the positive square root of 256, the negative square root of 256, or both? Explain.

Solution

Problem 19 :

The area of the base of a square notepad is 9 square inches. What is the length of one side of the base of the notepad?

Solution

Problem 20 :

The kinetic energy K (in joules) of a falling apple is represented by K = v²/2 , where v is the speed of the apple (in meters per second). How fast is the apple traveling when the kinetic energy is 32 joules?

Solution

Problem 21 :

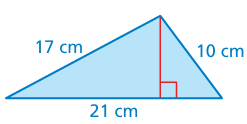
The area of the triangle is represented by the formula A = √s(s − 21)(s − 17)(s − 10) , where s is equal to half the perimeter. What is the height of the triangle?

Solution

Adding and subtracting Radical Expressions

Problem 1 :

3√6 - 4√6

Solution

Problem 2 :

-3√7 + 4√7

Solution

Problem 3 :

-11√21 - 11√21

Solution

Problem 4 :

-9√15 + 10√15

Solution

Problem 5 :

-10√7 + 12√7

Solution

Problem 6 :

-3√17 - 4√17

Solution

Problem 7 :

-10√11 - 11√11

Solution

Problem 8 :

-2√3 + 3√27

Solution

Problem 9 :

2√6 - 2√24

Solution

Problem 10 :

2√6 + 3√54

Solution

Problem 11 :

-√12 + 3√3

Solution

Problem 12 :

3√3 - √27

Solution

Problem 13 :

3√8 + 3√2

Solution

Problem 14 :

-3√6 + 3√6

Solution

Find the perimeter of the shapes given below.

Problem 15 :

Solution

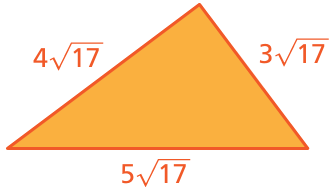
Problem 16 :

Solution

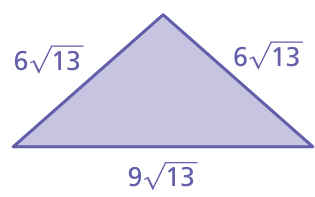
Problem 17 :

Solution

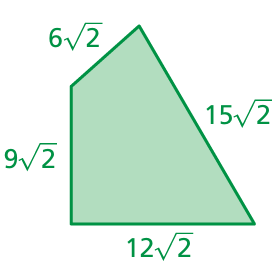
Problem 18 :

Solution

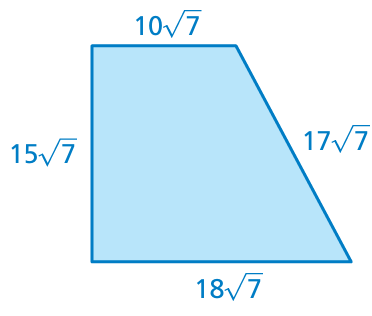
Problem 19 :

What are the perimeter and area of a rectangle with length of 5√3 cm and width of 3√2 cm ?

Solution

Problem 20 :

The sum of 2√8, 4√50 and 3√18 is

Solution

Problem 21 :

The difference between (1/2) √180 and (2/5) √20

Solution

Multiplying Radical Expressions

Question :

1)  √6 × 4√6

2)  -√5 × √20

3)  -√2 × √3

4)  4√8 × √2

5)  √12×√15

6)  √5 × (-2√5)

7)  -3√5 ×√20

8)  √15 × 3√5

9)  √9 ×√3

10)  -4√8 ×√10

Solution

Simplify each expression.

Problem 1 :

√600

Solution

Problem 2 :

√50 + √18

Solution

Problem 3 :

(5√6)²

Solution

Problem 4 :

√3(√3 + √6)

Solution

Problem 5 :

√19²

Solution

Problem 6 :

√64 + 36

Solution

Problem 7 :

√2(√2 + √6)

Solution

Problem 8 :

√2(√3 + √8)

Solution

Problem 9 :

√36/324

Solution

Problem 10 :

√50/√2

Solution

Problem 11 :

8√25/4

Solution

Problem 12 :

√16/4

Solution

Problem 13 :

2√2 [3/√2 + √2]

Solution

Problem 14 :

A rectangle has width 3√5 cm and length 4√10 cm. Find the area of rectangle.

Solution

Problem 15 :

A rectangle has length √(a/8) meters and width √(a/2) m. What is the area of rectangle ?

Solution

Problem 16 :

The formula for area A of a square with side length s is A = s². Solve the equation for s, and find the side length of a square having an area of 72 square inches

Solution

Problem 17 :

If x = 81b² and b > 0, the find √x = 

a)  -9b       b)  9b     c)  3b√27      d)  27b√3

Solution

Problem 18 :

Find the area of the rectangle in simplest form.

Solution

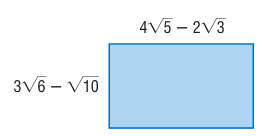
Problem 19 :

Find the perimeter and area of square whose sides measure 4 + 3√6 feet.

Solution

Problem 20 :

The voltage V is required for a circuit is given by V = √PR, where P is power in watts and R is the resistance in ohms. How many more volts area needed to light a 100 watt bulb than a 75 watt bulb if the resistance for both is 110 ohms.

Solution