SIMPLIFYING RADICAL EXPRESSIONS

Simplify each expression.

Problem 1 :

√600

Solution :

= √600

= √100 × 6

= √100 × √6

= 10√6

Problem 2 :

√50 + √18

Solution :

= √50 + √18

= √ (25 × 2) + √ (9 × 2)

= 5√2 + 3√2

= 8√2

Problem 3 :

(5√6)²

Solution :

= (5√6)²

= 5² × (√6)²

= 25 × 6

= 150

Problem 4 :

√3(√3 + √6)

Solution :

= √3(√3 + √6)

= (√3 × √3) + (√3 × √6)

= 3 + √18

= 3 + √ (9 × 2)

= 3 + √9 × √2

= 3 + 3√2

Problem 5 :

√19²

Solution :

= √19²

= √19 × 19

= 19

Problem 6 :

√64 + 36

Solution :

= √64 + 36

= √64 + √36

= 8 + 6

= 14

Problem 7 :

√2(√2 + √6)

Solution :

= √2(√2 + √6)

= (√2 × √2) + (√2 × √6)

= 2 + √12

= 2 + √ (4 × 3)

= 2 + √4 × √3

= 2 + 2√3

Problem 8 :

√2(√3 + √8)

Solution :

= √2(√3 + √8)

= (√2 × √3) + (√2 × √8)

= √6 + √16

= √6 + √ (4 × 4)

= √6 + √4 × √4

= √6 + 4

= 4 + √6

Problem 9 :

√36/324

Solution :

= √36/324

= √36/√324

= 6/18

= 1/3

Problem 10 :

√50/√2

Solution :

= √50/√2

= √50/2

= √25

= 5

Problem 11 :

8√25/4

Solution :

= 8√25/4

= 8 (√25/√4)

= 8 × 5/2

= 4 × 5

= 20

Problem 12 :

√16/4

Solution :

= √16/4

= √16/√4

= 4/2

= 2

Problem 13 :

2√2 [3/√2 + √2]

Solution :

= 2√2 [3/√2 + √2]

= 2√2 × [(3√2/√2 × √2) + √2]

= 2√2 (3√2/2 + √2)

= 2√2 [(3√2 + 2√2)/2]

= √2 (3√2 + 2√2)

= √2 × 5√2

= 2 × 5

= 10

Problem 14 :

A rectangle has width 3√5 cm and length 4√10 cm. Find the area of rectangle.

Solution :

Length = 4√10 cm

Width = 3√5 cm

Area of rectangle = length x width

= 4√10(3√5)

= 12√(10 x 5)

= 12√(2 x 5 x 5)

= 12 x 5√2

= 60√2

Problem 15 :

A rectangle has length √(a/8) meters and width √(a/2) m. What is the area of rectangle ?

Solution :

Length = √(a/8) meters

Width = √(a/2) meters

Area of rectangle = length x width

= √(a/8) √(a/2)

= √(a/8)(a/2)

= a√(1/4 x 4)

= a/4 cm²

Problem 16 :

The formula for area A of a square with side length s is A = s². Solve the equation for s, and find the side length of a square having an area of 72 square inches.

Solution :

Area A = s²

Given that, the area is 72 square inches

72 = s²

s = √72

s = √(2 x 2 x 2 x 3 x 3)

= 2 x 3√2

= 6 √2 inches

Problem 17 :

If x = 81b² and b > 0, the find √x = 

a)  -9b       b)  9b     c)  3b√27      d)  27b√3

Solution :

Given that, x = 81b²

√x = √81b²

√x = √(9 x 9 x b x b)

√x = 9b

So, option b is correct.

Problem 18 :

Find the area of the rectangle in simplest form.

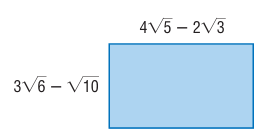
Solution :

Length = 4√5 - 2√3

Width = 3√6 - √10

Area of rectangle = length x width

= (4√5 - 2√3) (3√6 - √10)

= 4√5(3√6) - 4√5(√10) - 2√3(3√6) + 2√(3 x 10)

= 12√30 - 4√(5 x 10) - 6√(3 x 6) + 2√30

= 12√30 - 4√(5 x 5 x 2) - 6√(3 x 3 x 2) + 2√30

= 12√30 + 2√30 - (4x5)√2 - (6 x 3)√2

= 14√30 - 20√2 - 18√2

= (14√30 - 38√2) square units.

Problem 19 :

Find the perimeter and area of square whose sides measure 4 + 3√6 feet.

Solution :

Side length of square = 4 + 3√6 feet.

Perimeter of square = 4(side)

= 4(4 + 3√6)

= 16 + 12√6 feet

Area of square = (4 + 3√6)²

= 4² + 2(4)3√6 + (3√6)²

= 16 + 24√6 + 9(6)

= 16 + 24√6 + 54

= 70 + 24√6 square feet.

Problem 20 :

The voltage V is required for a circuit is given by V = √PR, where P is power in watts and R is the resistance in ohms. How many more volts area needed to light a 100 watt bulb than a 75 watt bulb if the resistance for both is 110 ohms.

Solution :

V = √PR

When P = 100 watt and R = 110 ohms

V = √(100 x 110)

= √11000

= 104.88

V = √PR

When P = 75 watt and R = 110 ohms

V = √(75 x 110)

= √8250

= 90.82

Difference = 104.88 - 90.82

= 14.06 V