HOW TO ADD AND SUBTRACT RADICAL EXPRESSIONS

To add and subtract radical expressions, we should know about like radicals and unlike radicals.

Unlike radical :

We will not have same value inside the radical sign, or we will not have same index.

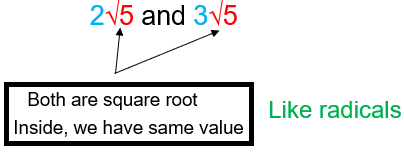
Like radical :

It means we should have the same numerical value inside the radical sign with the same index.

In front of radical sign, we may see same value or different value that doesn't matter.

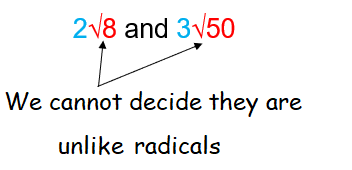
By decomposing 8 and 50, we get 

√8 = √(2 x 2 x 2) = 2√2

√50 = √(2 x 5 x 5) = 5√2

After simplification, we get the same values inside the radical sign. So, they are unlike radicals.

Problem 1 :

3√6 - 4√6

Solution :

Inside the radical signs, radicands are like terms. we can combine them.

= 3√6 - 4√6

= (3 - 4)√6

= -√6

Problem 2 :

-3√7 + 4√7

Solution :

Inside the radical signs, radicands are like terms. we can combine them.

= (-3 + 4)√7

= √7

Problem 3 :

-11√21 - 11√21

Solution :

Inside the radical signs, the radicands are like terms. we can combine them.

= (-11 - 11)√21

= -22√21

Problem 4 :

-9√15 + 10√15

Solution :

= (-9 + 10)√15

= √15

Problem 5 :

-10√7 + 12√7

Solution :

= (-10 + 12)√7

= 2√7

Problem 6 :

-3√17 - 4√17

Solution :

= (-3 - 4)√17

= -7√17

Problem 7 :

-10√11 - 11√11

Solution :

= (-10 - 11)√11

= -21√11

Problem 8 :

-2√3 + 3√27

Solution :

Here the radicands are unlike terms.

Since 3 is a prime number, we cannot decompose 3 hereafter.

So, we are decomposing 27 into prime factors.

= -2√3 + 3√(3×3×3)

= -2√3 + 3∙3√3

= -2√3 + 9√3

= (-2+9)√3

= 7√3

Problem 9 :

2√6 - 2√24

Solution :

Here the radicands are unlike terms.

We cannot decompose 6 hereafter. So, we are decomposing 24 into prime factors.

= 2√6 - 2√(2×2×2×3)

= 2√6 - 2×2√(2×3)

= 2√6 - 4√6

= (2 - 4)√6

= -2√6

Problem 10 :

2√6 + 3√54

Solution :

Here the radicands are unlike terms. 

We cannot decompose 6 hereafter. So, we are decomposing 54 into prime factors.

= 2√6 + 3√(3×3×3×2)

 = 2√6 + 3×3√(3×2)

 = 2√6 + 9√6

= (2+9)√6

= 11√6

Problem 11 :

-√12 + 3√3

Solution :

Here the radicands are unlike terms.

We cannot decompose 3 hereafter. So, we are decomposing 12 into prime factors.

= √(2×2×3) + 3√3

= -2√3 + 3√3

= (-2+3)√3

= √3

Problem 12 :

3√3 - √27

Solution :

Here the radicands are unlike terms.

We cannot decompose 3 hereafter. So, we are decomposing 27 into prime factors.

= 3√3 - √(3×3×3)

= 3√3 - 3√3

= 0

Problem 13 :

3√8 + 3√2

Solution :

Here the radicands are unlike terms.

We cannot decompose 2 hereafter. So, we are decomposing 8 into prime factors.

= 3√(2×2×2) + 3√2

= 3×2√2 + 3√2

= 6√2 + 3√2

= (6 + 3)√2

= 9√2

Problem 14 :

-3√6 + 3√6

Solution :

= -3√6 + 3√6

= 0

Find the perimeter of the shapes given below.

Problem 15 :

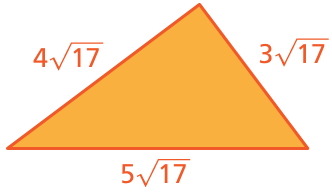
Solution :

Perimeter = sum of length of all sides

= 4√17 + 3√17 + 5√17

Since everything is like radicals, 

= 12√17

So, the perimter of the triangle is 12√17.

Problem 16 :

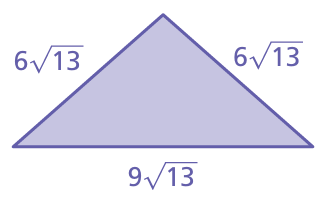
Solution :

Perimeter = sum of length of all sides

= 6√13 + 6√13 + 9√13

= 21√13

So, the perimeter of the triangle is 21√13.

Problem 17 :

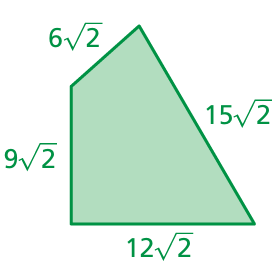
Solution :

Perimeter = sum of length of all sides

= 6√13 + 6√13 + 9√13

= 21√13

So, the perimeter of the triangle is 21√13.

Problem 18 :

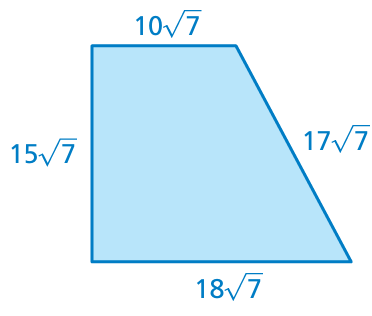
Solution :

Perimeter = sum of length of all sides

= 15√7 + 18√7 + 17√7 + 10√7

= 60√7

So, the perimeter of the quadrilateral is 60√7

Problem 19 :

What are the perimeter and area of a rectangle with length of 5√3 cm and width of 3√2 cm ?

Solution :

Perimeter of rectangle = 2(length + width)

Length = 5√3 cm and width = 3√2 cm

Perimeter of rectangle = 2(5√3 + 3√2)

= (10√3 + 6√2) cm

Area of rectangle = length x width

= 5√3(3√2)

= 15√(3 x 2)

= 15√6 cm²

Problem 20 :

The sum of 2√8, 4√50 and 3√18 is

Solution :

Sum of 2√8, 4√50 and 3√18

= 2√8 + 4√50 + 3√18

= 2√(2⋅2⋅2) + 4√(2⋅5⋅5) + 3√(2⋅3⋅3)

= 2(2)√2 + 4(5)√2 + 3(3)√2

= 4√2 + 20√2 + 9√2

= 33√2

Problem 21 :

The difference between (1/2) √180 and (2/5) √20

Solution :

= (1/2) √180 - (2/5) √20

= (1/2) √(2 x 2 x 5 x 3 x 3) - (2/5) √(2 x 2 x 5)

= (1/2) (2 x 3)√5 - (2/5) x 2√5

= (1/2) (6)√5 - (4/5)√5

= 3√5 - (4/5)√5

= [(15 - 4) / 5 ]√5

= 11√5/5