HOW TO MULTIPLY RADICAL EXPRESSIONS

Problem 1 :

√6 × 4√6

Solution :

Using the property, a√b × c√b= (a×c)√b√b

√6 × 4√6 = (1×4)√(6×6)

Since we see two same values inside the radical sign, we take one out of it.

= 4 × 6

= 24

Problem 2 :

-√5 × √20

Solution :

-√5 × √20 = √(5 x 20)

= -√(5 × 5 × 2 × 2)

We see two 5’s and  2’s. So, take one out of it.

= -5×2

= -10

Problem 3 :

-√2 × √3

Solution :

-√2 × √3 = (-1 × 1)√(2 × 3)

Since we see the different values inside the radical sign, multiply it.

= -√6

Problem 4:

4√8 × √2

Solution :

4√8 × √2 = 4√(8x2)

= (4×1)√(2×2×2×2)

2 is repeated 4 times, so take two 2's. 

= 4×2×2

= 16

Problem 5 :

√12×√15

Solution :

√12 × √15 = √(12 × 15)

= √(2 × 2 × 3 × 3 × 5)

We see two 2’s and 3’s and once 5. so take one out of it.

= 2 × 3√5

= 6√5

Problem 6 :

√5 × (-2√5)

Solution :

√5×-2√5 = (-2 × 1)√(5 × 5)

Since we see two same values inside the radical sign, we take one out of it. 

= -2 × 5

= -10

Problem 7 :

-3√5 ×√20

Solution :

-3√5×√20 = (-3×1)√(5 × 20)

= (-3×1)√(5 × 5 × 2 × 2)

We see two 5’s and  2’s. so take one out of it.

= -3 × 5 × 2

= -30

Problem 8 :

√15 × 3√5

Solution :

√15×3√5 = (3×1) √(15 × 5)

= 3√(3 × 5 × 5)

We see two 5’s and one 3.

= 3×5√3

=15√3

Problem 9 :

√9 ×√3

Solution :

√9×√3 = √(9 × 3)

= (3 ×  3 × 3)

For two same 3's, we take one out of the radical.

= 3√3

Problem 10 :

-4√8 ×√10

Solution :

-4√8 × √10 = (-4 × 1)√(8 × 10)

= (-4×1)√(2 × 2 × 2 × 2 × 5)

= -4 × 2 × 2√5

= -16√5

Problem 11 :

Express (√3 - √2)² in simplest form.

Solution :

(√3 - √2)²

Using algebraic identity (a - b)² = a² - 2ab + b²

(√3 - √2)² = √3² - 2√3√2 + √2²

= 3 - 2√(3 x 2) + 2

= 5 - 2√6

Problem 12 :

The radius of the circle is 3√5 cm. If a square is inscribed in a circle 

a) determine tehe exact length of the diagonal of a square

b)  Determine the exact perimeter of the square.

Solution :

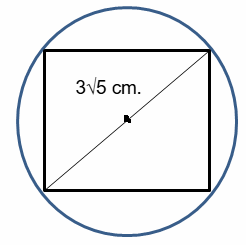
a) Length of the diagonal = 2 x radius

= 2 x 3√5

= 6√5 cm

b) Perimeter of square 

Let x be the side length of the square.

diagonal² = x² + x² 

(6√5)² = 2x²

36(5) = 2x²

x² = 18(5)

x = √90

x = √3 x 3 x 10

x = 3√10

Area of square = x (x)

= x²

= 90 cm²

Problem 13 :

The length of a rectangle is 2 √48 and width is 6√3. Express in the simplest form.

a) The area of the rectangle

b) The perimeter of the rectangle.

Solution :

a)  

Length = 2 √48

Width = 6√3

Area of rectangle = length x width

= 2√48 (6√3)

= 12√(48 x 3)

= 12√(4 x 4 x 3 x 3)

= 12 x 4 x 3

= 144 square units

b) Perimeter of rectangle = 2(length + width)

= 2(2√48 + 6√3)

= 2(2√(4 x 4 x 3 x 3) + 6√3)

= 2 (24 + 6√3)

= 2(6)(4 + √3)

= 12(4 + √3) units.

Problem 14 :

The area of the rectangle is 20√50 and length is 4√2, what is the width ?

Solution :

Area of rectangle = length x width

Area of rectangle = 20√50, length = 4√2, width = x(assuming)

20√50 = 4√2 ⋅ x

x = 20√50 / 4√2

x = 5(√50 / √2)

x = 5(√(5⋅5⋅2) / √2)

= 5⋅5(√2/√2)

= 25

So, the width of the rectangle is 25 units.

Problem 15 :

If the perimeter of the rectangle is 12√3 and the length is 2√12, what is the width ?

Solution :

Perimeter of rectangle = 12√3

length = 2√12

Width = x(Assuming)

12√3 = 2(2√12 + x)

12√3/2 = (2√12 + x)

6√3 = (2√12 + x)

x = 6√3 - 2√12

= 6√3 - 2√(2 x 2 x 3)

= 6√3 - 2 x 2√3

= 6√3 - 4√3

= 2√3 units.

Problem 16 :

The area of the parallelogram is 8√90 and the base is 2√5. What is the height of the parallelogram ?

Solution :

Area of parallelogram = base ⋅ height

Let x be the height of the parallelogram.

8√90 = 2√5 ⋅ x

x = 8√90/2√5

= 4(√90/√5)

= 4(√3 ⋅ 3 ⋅ 2 ⋅ 5)/√5)

= (4 ⋅ 3)(√10/√5)

= 12√10/√5

To rationalize the denominator, we have to multiply by √5 in both numerator and denominator.

= 12(√10 / √5) ⋅ (√5/√5)

= 12(√10√5 / 5)

= (12 ⋅ 5) √2/5

= 12√2