PERIMETER OF SHAPES INVOLVING POLYNOMIALS WORKSHEET

Find the perimeter P of the following given all sides are measured in cm:

Problem 1:

Solution

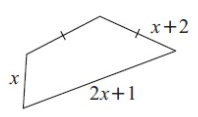
Problem 2 :

Solution

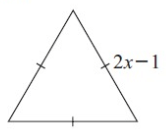
Problem 3 :

Solution

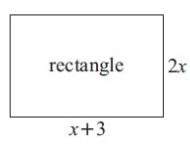
Problem 4 :

Solution

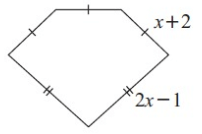
Problem 5 :

Solution

Problem 6 :

Solution

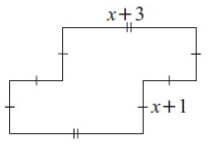
Problem 7 :

Solution

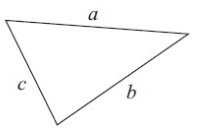
Problem 8 :

Solution

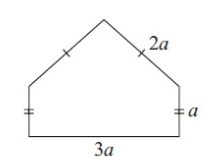
Problem 9 :

Solution

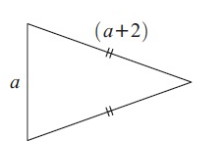
Problem 10 :

A magician’s stage has a trapdoor.

a. The total area (in square feet) of the stage can be represented by

x² + 27x + 176

Write an expression for the width of the stage.

b. Write an expression for the perimeter of the stage.

c. The area of the trapdoor is 10 square feet. Find the value of x.

d. The magician wishes to have the area of the stage be at least 20 times the area of the trapdoor. Does this stage satisfy his requirement? Explain.

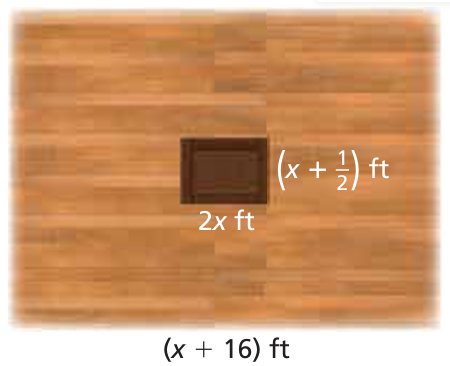
Problem 11 :

You are playing miniature golf on the hole shown.

a. Write a polynomial that represents the area of the golf hole.

b. Write a polynomial that represents the perimeter of the golf hole.

c. Find the perimeter of the golf hole when the area is 216 square feet.

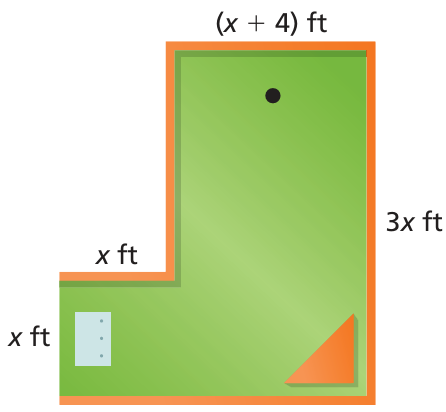
Problem 12 :

Write the polynomial in standard form that represents the perimeter of the quadrilateral.

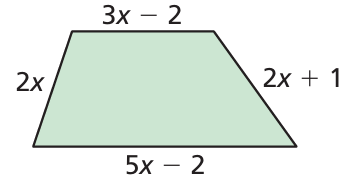
Problem 13 :

You are making a blanket with a fringe border of equal width on each side.

a. Write a polynomial that represents the perimeter of the blanket including the fringe.

b. Write a polynomial that represents the area of the blanket including the fringe.

c. Find the perimeter and the area of the blanket including the fringe when the width of the fringe is 4 inches.

Find the perimeter of the shapes given below.

Problem 1 :

Solution

Problem 2 :

Solution

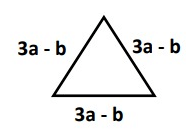
Problem 3 :

Solution

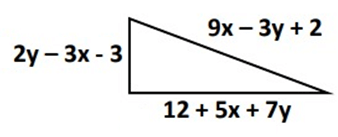
Problem 4 :

Solution

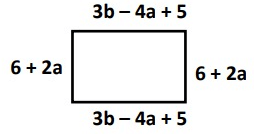
Problem 5 :

Solution

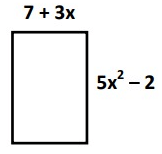
Problem 6 :

Solution

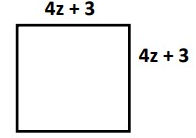
Problem 7 :

Solution

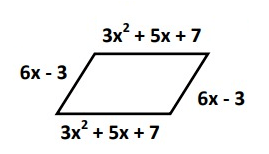
Problem 8 :

Solution

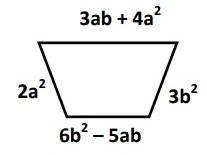
Problem 9 :

Solution

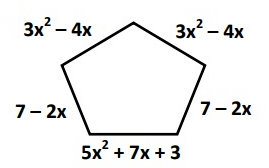
Problem 10 :

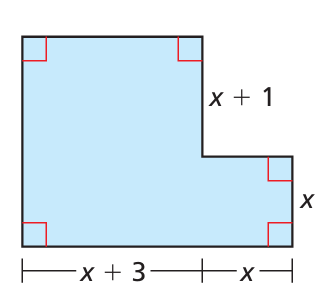
Adjoin one or more polygons to the rectangle to form a single new polygon whose perimeter is double that of the rectangle. Find the perimeter of the new polygon.

Solution

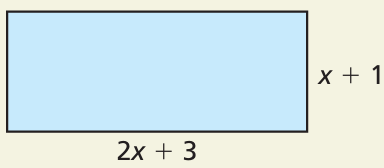
Problem 11 :

Write an expression for the area and perimeter for the figure shown.

Solution

Problem 12 :

A projector displays an image on a wall. The area (in square feet) of the projection is represented by x² − 8x + 15.

a. Write a binomial that represents the height of the projection.

b. Find the perimeter of the projection when the height of the wall is 8 feet.

Solution

Problem 13 :

The length of a rectangle is 1 inch more than twice its width. The value of the area of the rectangle (in square inches) is 5 more than the value of the perimeter of the rectangle (in inches). Find the width.

Solution

Express the area of the figure as a polynomial in descending powers of the variable x.

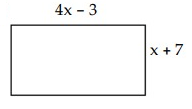
Problem 1 :

Solution

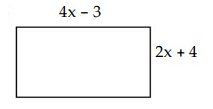
Problem 2 :

Solution

Problem 3 :

The area of a rectangle is 20m² – 13m – 15. Find the length if the width is 4m – 5.

Solution

Problem 4 :

A rectangular patio has an area of 2m³ + 12m² + 6m – 40. Find the length if the width is 2m + 8.

Solution

Find simplified expressions for the perimeter and area of the given figure.

Problem 5 :

Solution

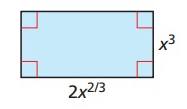
Problem 6 :

Solution

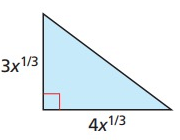
Problem 7 :

The area of a rectangular window is (2x² – 7x – 15). Both the length and the width are polynomials with integer coefficients. Which of the following could represent the length of the window?

Solution

Problem 8 :

A triangle is inscribed in a square, as shown. Write and simplify a function r in terms of x that represents the area of the shaded region.

Solution

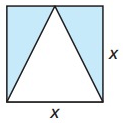
Problem 9 :

The composite solid is made up of a cube and a rectangular prism

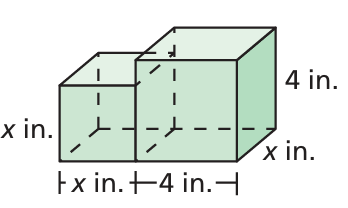
a. Write a polynomial that represents the volume of the composite solid.

b. The volume of the composite solid is equal to 25x. What is the value of x? Explain your reasoning.

Solution

Problem 10 :

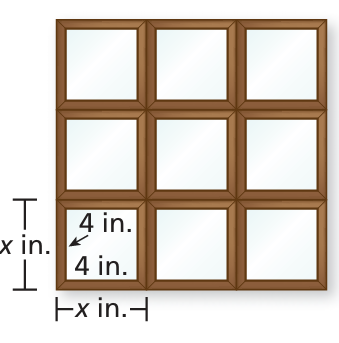
You hang nine identical square picture frames on a wall.

a. Write a polynomial that represents the area of the picture frames, not including the pictures.

b. The area in part (a) is 81 square inches. What is the side length of one of the picture frames? Explain your reasoning.

Solution