WORD PROBLEMS INVOLVING POLYNOMIAL

Express the area of the figure as a polynomial in descending powers of the variable x.

Problem 1 :

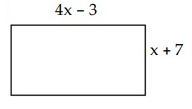
Solution :

Area of a rectangle = l × w

By observing the figure,

 l = 4x – 3, w = x + 7

Area of the rectangle = (4x – 3) (x + 7)

= 4x² + 28x – 3x -  21

= 4x² + 25x - 21

Problem 2 :

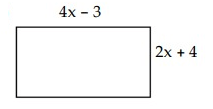
Solution :

Area of a rectangle = l × w

By observing the figure,

 l = 4x – 3, w = 2x + 4

= (4x – 3)(2x+ 4)  

= 8x² + 16x - 6x – 12

= 8x² + 10x - 12

Problem 3 :

The area of a rectangle is 20m² – 13m – 15. Find the length if the width is 4m – 5.

Solution :

Given, 20m² – 13m – 15

Length = ? and width = 4m - 5

Area of a rectangle = l × w

20m² – 13m – 15 = l × (4m – 5)

(20m² – 13m – 15)/(4m – 5) = l

(20m² – 13m – 15) = (4m – 5) (10m + 6)

 (4m – 5) (5m + 3)/ (4m – 5) = l

 5m + 3 = l

So, the length is 5m + 3.

Problem 4 :

A rectangular patio has an area of 2m³ + 12m² + 6m – 40. Find the length if the width is 2m + 8.

Solution :

Given, 2m³ + 12m² + 6m – 40

Length = ? and width = 2m + 8

Area of a rectangle = l × w

2m³ + 12m² + 6m – 40= l × (2m + 8)

(2m³ + 12m² + 6m – 40)/(2m + 8) = l

(m³ + 6m² + 3m – 20)/(m + 4) = l

Using long division method,

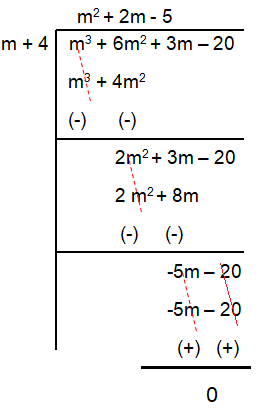
(2m³ + 12m² + 6m – 40)/(2m + 8) = m² + 2m - 5

So, the length is m² + 2m - 5.

Find simplified expressions for the perimeter and area of the given figure.

Problem 5 :

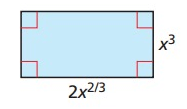
Solution :

By observing the figure,

l = 2x^2/3, w = x³

Perimeter of a rectangle = 2(l + w)

= 2(2x^2/3 + x³)

= 4x^2/3 + 2x³

Area of a rectangle = l × w

= (2x^2/3 × x³)

= 2x^{(2/3 + 3)}

= 2x^(11/3)

Problem 6 :

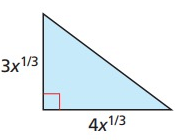
Solution :

By observing the figure,

Base (b) = 4x^1/3, height (h) = 3x^1/3

Area of triangle = 1/2 b × h

= 1/2 (4x^1/3) × (3x^1/3)

= 1/2 (12x^2/3)

= 6x^2/3

So, area of triangle is 6x^2/3.

Perimeter of right angle triangle

Using Pythagorean theorem

a² + b² = c²

a = 3x^1/3 and b = 4x^1/3

(3x^1/3)² + (4x^1/3)²  = c²

9x^2/3 + 16x^2/3 = c²

25x^2/3 = c²

c² = (5x^1/3)²

c = 5x^1/3

Perimeter of the triangle = 3x^1/3 + 4x^1/3 + 5x^1/3

= 12x^1/3

Problem 7 :

The area of a rectangular window is (2x² – 7x – 15). Both the length and the width are polynomials with integer coefficients. Which of the following could represent the length of the window? 

Solution :

Area of a rectangular window = (2x² – 7x – 15).

The length and the width are polynomials with integer coefficients.

= 2x² – 7x – 15

= 2x² – 10x + 3x – 15

= 2x(x – 5) + 3(x – 5)

= (2x+ 3) (x – 5)

So, the length of the window is 2x + 3.

Problem 8 :

A triangle is inscribed in a square, as shown. Write and simplify a function r in terms of x that represents the area of the shaded region.

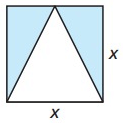
Solution :

Area of a square A = S²

= x²

Area of triangle = (1/2) b × h

= 1/2 (x²)

Area of the shaded region = area of the square  - area of the unshaded region

Area of the unshaded region is using area of the triangle.

= x² – 1/2 x²

= x²(1 – 1/2)

= x²((2 – 1)/2)

= 1/2 x²

Problem 9 :

The composite solid is made up of a cube and a rectangular prism.

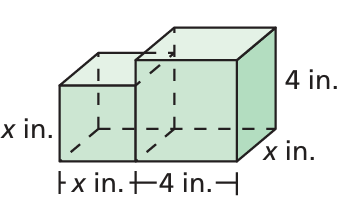
a. Write a polynomial that represents the volume of the composite solid.

b. The volume of the composite solid is equal to 25x. What is the value of x? Explain your reasoning.

Solution :

a) Volume of composite solid = volume of square prism + volume of rectangular prism

= x³ + 4x(4)

= x³ + 16x

b)  Volume of composite solid = 25x

x³ + 16x = 25x

x³ + 16x - 25x = 0

x³ - 9x = 0

x(x² - 9) = 0

x(x² - 3²) = 0

x(x + 3)(x - 3) = 0

x = 0, x = 3 and x = -3

The value of x must be 3.

Problem 10 :

You hang nine identical square picture frames on a wall.

a. Write a polynomial that represents the area of the picture frames, not including the pictures.

b. The area in part (a) is 81 square inches. What is the side length of one of the picture frames? Explain your reasoning.

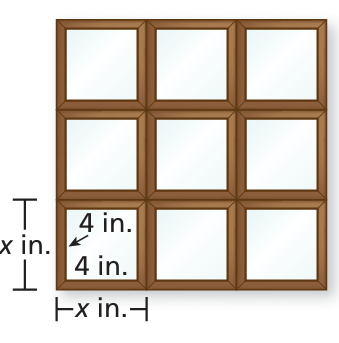
Solution :

Side length of picture frame = 3x

Area of one picture = 16 square inches

Area of 9 pictures = 9(16)

= 144 square inches

a) Area of picture frame not including pictures = (3x)(3x) - 144

= 9x² - 144

b) 9x² - 144 = 81

9x² - 144 - 81 = 0

9x² - 225 = 0

9x² - 15² = 0

(3x)² - 15² = 0

(3x + 15)(3x - 15) = 0

3x + 15 = 0 and 3x - 15 = 0

3x = -15 and 3x = 15

x = -5 and x = 5

Side length of window = 3(5) ==> 15 inches