FIND THE PERIMETER WITH POLYNOMIALS

Find the perimeter of the shapes given below.

Problem 1 :

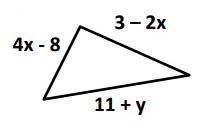
Solution : 

Perimeter = Sum of all the sides

= (4x - 8) + (3 – 2x) + (11 + y)

= 4x – 8 + 3 – 2x + 11 + y

= 4x – 2x + y – 8 + 3 + 11

= 2x + y + 6

Problem 2 :

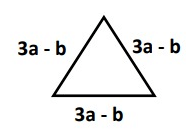
Solution :

Perimeter = Sum of all the sides

= (3a - b) + (3a - b) + (3a - b)

= 3a – b + 3a – b + 3a – b

= 3a + 3a + 3a – b – b – b

= 9a – 3b

Problem 3 :

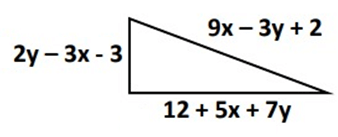
Solution :

Perimeter = Sum of all the sides

= (2y – 3x - 3) + (9x – 3y + 2) + (12 + 5x + 7y)

= 2y – 3x - 3 + 9x – 3y + 2 + 12 + 5x + 7y

= 2y – 3y + 7y – 3x + 9x + 5x – 3 + 2 + 12

= 6y + 11x + 11

Problem 4 :

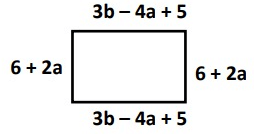
Solution :

Perimeter = Sum of all the sides

= (6 + 2a) + (3b – 4a + 5) + (6 + 2a) + (3b – 4a + 5)

= 6 + 2a + 3b – 4a + 5 + 6 + 2a + 3b – 4a + 5

= 2a – 4a + 2a – 4a + 3b + 3b + 6 + 5 + 6 + 5

= -4a + 6b + 22

Problem 5 :

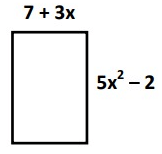
Solution :

Perimeter = Sum of all the sides

= (7 + 3x) + (5x² - 2) + (7 + 3x) + (5x² - 2)

= 7 + 3x + 5x² - 2 + 7 + 3x + 5x² - 2

= 5x² + 5x² + 3x + 3x + 7 + 7 – 2 – 2

= 10x² + 6x + 10

Problem 6 :

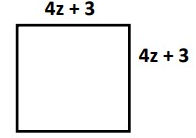
Solution :

Perimeter = Sum of all the sides

= (4z + 3) + (4z + 3) + (4z + 3) + (4z + 3)

= 4z + 3 + 4z + 3 + 4z + 3 + 4z + 3

= 4z + 4z + 4z + 4z + 3 + 3 + 3 + 3

= 16z + 12

Problem 7 :

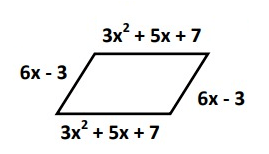
Solution :

Perimeter = Sum of all the sides

= (3x² + 5x + 7) + (6x - 3) + (3x² + 5x + 7) + (6x - 3)

= 3x² + 5x + 7 + 6x - 3 + 3x² + 5x + 7 + 6x – 3

= 3x² + 3x² + 5x + 6x + 5x + 6x + 7 + 7 – 3 – 3

= 6x² + 22x + 8

Problem 8 :

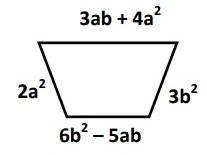
Solution :

Perimeter = Sum of all the sides

= 2a² + 3ab + 4a² + 3b² + 6b² - 5ab

= 2a² + 4a² + 3b² + 6b² + 3ab – 5ab

= 6a² + 9b² - 2ab

Problem 9 :

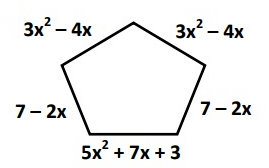
Solution :

Perimeter = Sum of all the sides

= 7 – 2x + 3x² - 4x + 3x² - 4x + 7 – 2x + 5x² + 7x + 3

= 3x² + 3x² + 5x² - 2x – 4x – 4x – 2x + 7x + 7 + 7 + 3

= 11x² - 5x + 17

Problem 10 :

Adjoin one or more polygons to the rectangle to form a single new polygon whose perimeter is double that of the rectangle. Find the perimeter of the new polygon.

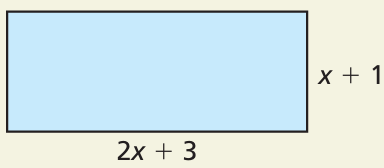
Solution :

Perimeter of the given rectangle = 2(length + width)

= 2(2x + 3 + x + 1)

= 2(3x + 4)

= 6x + 8

Perimeter of new polygon = 2(perimeter of rectangle)

= 2(6x + 8)

= 12x + 16

Problem 11 :

Write an expression for the area and perimeter for the figure shown.

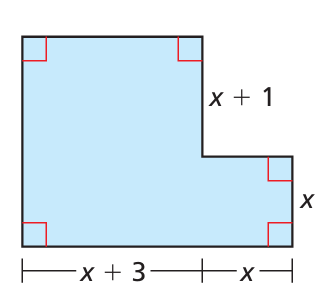
Solution :

Length of the rectangle towards the left = x + x + 1

= 2x + 1

Width of the rectangle at the left = x + 3

Side length of the square to the right = x

Area of the figure = (2x + 1)(x + 3) + x (x)

= 2x²+ 6x + 2x + 3 + x²

= 3 x² + 8x + 3

Perimeter of figure = 2[(x + 3) + (x + 1 + 1)] + 4x

= 2[x + 3 + x + 2] + 4x

= 2[2x + 5] + 4x

= 4x + 10 + 4x

= 8x + 10

Problem 12 :

A projector displays an image on a wall. The area (in square feet) of the projection is represented by x² − 8x + 15.

a. Write a binomial that represents the height of the projection.

b. Find the perimeter of the projection when the height of the wall is 8 feet.

Solution :

a) Area of projection = x² − 8x + 15

Factoring the polynomial, we get

= x² − 5x - 3x + 15

= x(x - 5) - 3(x - 5)

= (x - 5)(x - 3)

Shown width = (x - 3)

Then height of the projection = x - 5

b) Perimeter of the projection, wen height of the wall (x) = 8 ft

Perimeter = 2(x - 5 + x - 3)

= 2(2x - 8)

= 2(2(8) - 8)

= 2(16 - 8)

= 2(8)

= 16 ft

Problem 13 :

The length of a rectangle is 1 inch more than twice its width. The value of the area of the rectangle (in square inches) is 5 more than the value of the perimeter of the rectangle (in inches). Find the width.

Solution :

Let x be the width of the rectangle.

length = 2x + 1

Area of the rectangle = Perimeter of the rectangle + 5

= 2(x + 2x + 1) + 5

x(2x + 1) = 2(3x + 1) + 5

2x² + x = 6x + 2 + 5

2x² + x - 6x - 7 = 0

2x² - 5x - 7 = 0

2x² - 2x + 7x - 7 = 0

2x(x - 1) + 7(x - 1) = 0

(2x + 7)(x - 1) = 0

x = -7/2 and x = 1

So, the required width of the rectangle is 1.