PERIMETER OF SHAPES INVOLVING POLYNOMIALS

Find the perimeter P of the following given all sides are measured in cm:

Problem 1:

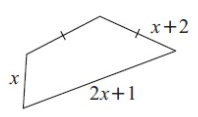
Solution :

Perimeter of the shape = 2(x + 2) + 2x + 1 + x

= 2x + 4 + 2x + 1 + x

= 5x + 5

So, the required perimeter is 5x + 5 cm.

Problem 2 :

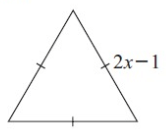
Solution :

The given figure is a triangle.

Perimeter of the triangle = a + b + c

= 2x - 1 + 2x - 1 + 2x - 1

= 6x - 3

So, perimeter of the triangle is 6x - 3 cm.

Problem 3 :

Solution : 

The given figure is a square.

Perimeter of the square = 4a

= 4(x + 4)

= 4x + 16

So, perimeter of the square is 4x + 16 cm.

Problem 4 :

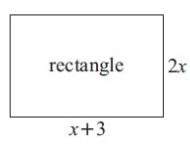
Solution :

The given figure is a rectangle.

Perimeter of the rectangle = 2(length + width)

Length = x + 3 and width = 2x

= 2(x + 3 + 2x)

= 2x + 6 + 4x

= 6x + 6

So, perimeter of the rectangle is 6x + 6 cm.

Problem 5 :

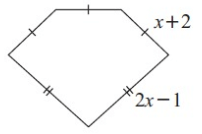
Solution :

Perimeter of the shape = 2(2x - 1) + 3(x + 2)

= 4x - 2 + 3x + 6

= 7x + 4

So, the required perimeter is 7x + 4 cm.

Problem 6 :

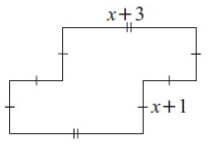
Solution :

Perimeter of the shape = 2(x + 3) + 6(x + 1)

= 2x + 6 + 6x + 6

= 8x + 12

So, the required perimeter is 8x + 12 cm.

Problem 7:

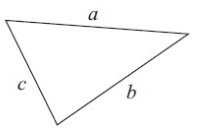
Solution :

The given figure is a triangle.

Perimeter of the triangle = a + b + c

So, perimeter of the triangle is a + b + c cm.

Problem 8 :

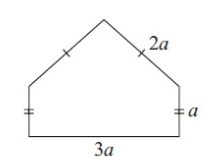
Solution :

Perimeter of the shape = 2(2a) + 2(a) + 3a

= 4a + 2a + 3a

= 9a

So, the required perimeter is 9a cm.

Problem 9 :

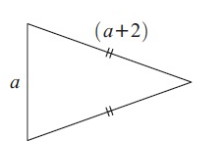
Solution :

Perimeter of the shape = 2(a + 2) + a

= 2a + 4 + a

= 3a + 4

So, the required perimeter is 3a + 4 cm.

Problem 10 :

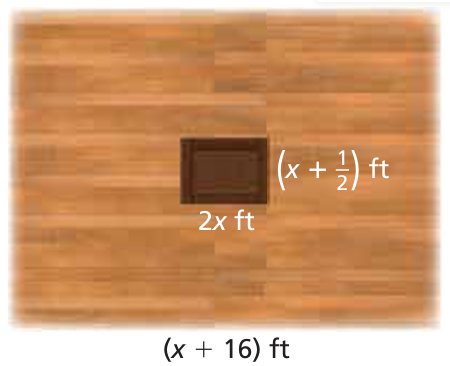
A magician’s stage has a trapdoor.

a. The total area (in square feet) of the stage can be represented by

x² + 27x + 176

Write an expression for the width of the stage.

b. Write an expression for the perimeter of the stage.

c. The area of the trapdoor is 10 square feet. Find the value of x.

d. The magician wishes to have the area of the stage be at least 20 times the area of the trapdoor. Does this stage satisfy his requirement? Explain.

Solution :

a) 

x² + 27x + 176

By factoring this polynomial, we will get product of linear factors in which one linear factor must be the length and another linear factor will be the width.

= x² + 16x + 11x + 176

= x(x + 16) + 11(x + 16)

= (x + 11)(x + 16)

Length = x + 11 and width = x + 16

b) Perimeter = 2(length + width)

= 2(x + 11 + x + 16)

= 2(2x + 27)

= 4x + 54

c) From the picture, length of trapdoor = 2x

width of trap door = x + 1/2

2x(x + 1/2) = 10

2x² + x = 10

2x² + x - 10 = 0

2x² - 4x + 5x - 10 = 0

2x(x - 2) + 5(x - 2) = 0

(2x + 5)(x - 2) = 0

x = -5/2 and x = 2

d) Area of the trapdoor = 10 square feet

Area of the stage = 20(10)

= 200 square feet

When x = 4

Area of stage = (4 + 11)(4 + 16)

= 15(20)

= 300

Yes, the stage satisfies the requirement because the total area ( sq ft) is more than 20 times the area of trapdoor.

Problem 11 :

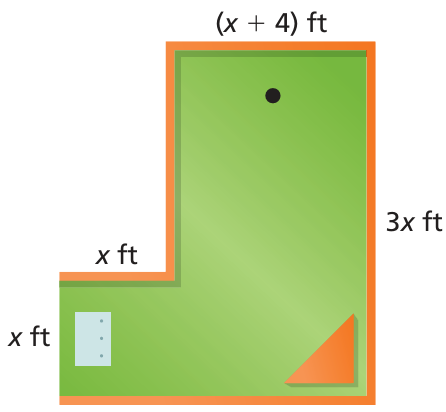
You are playing miniature golf on the hole shown.

a. Write a polynomial that represents the area of the golf hole.

b. Write a polynomial that represents the perimeter of the golf hole.

c. Find the perimeter of the golf hole when the area is 216 square feet.

Solution :

a. Area of golf hole = x(x) + 3x(x + 4)

= x² + 3x² + 12x

= 4x² + 12x

b. Perimeter of the golf hole = x + x + 2x + x + 4 + 3x + x + 4 + x

= 9x + 8

c. Given that, area = 216 square feet.

4x² + 12x = 216

4x² + 12x - 216 = 0

x² + 3x - 54 = 0

x² + 9x - 6x - 54 = 0

x(x + 9) - 6(x + 9) = 0

(x - 6)(x + 9) = 0

x = 6 and x = -9

Perimeter = 9x + 8

Applying x = 6, we get

= 9(6) + 8

= 54 + 8

= 62 feet

So, the required perimeter is 62 feet.

Problem 12 :

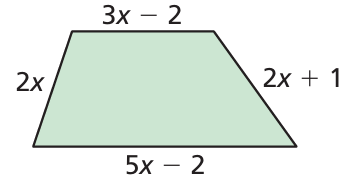
Write the polynomial in standard form that represents the perimeter of the quadrilateral.

Solution :

Perimeter = Sum of lengths of all sides

= 3x - 2 + 2x + 1 + 5x - 2 + 2x

= 12x - 4 + 1

= 12x - 3

Problem 13 :

You are making a blanket with a fringe border of equal width on each side.

a. Write a polynomial that represents the perimeter of the blanket including the fringe.

b. Write a polynomial that represents the area of the blanket including the fringe.

c. Find the perimeter and the area of the blanket including the fringe when the width of the fringe is 4 inches.

Solution :

a) Length of blanket including the fringe = 72 + 2x

Width of fringe = 48 + 2x

a) Perimeter of blanket = 2(72 + 2x + 48 + 2x)

= 2(120 + 4x)

= 240 + 8x inches

b) Area of the blanket = (72 + 2x) (48 + 2x)

= 3456 + 144x + 96x + 4x²

= 3456 + 240x + 4x²

= 4x² + 240x + 3456

c) When width x = 6

Perimeter = 240 + 8x

= 240 + 8(6)

= 240 + 48

= 288 inches

Area = 4x² + 240x + 3456

= 4(4)² + 240(4) + 3456

= 64 + 960 + 3456

= 4480 square inches