GRAPHING LINES USING X AND Y INTERCEPTS WORKSHEET

Use axes intercepts to draw the graph of:

Problem 1 :

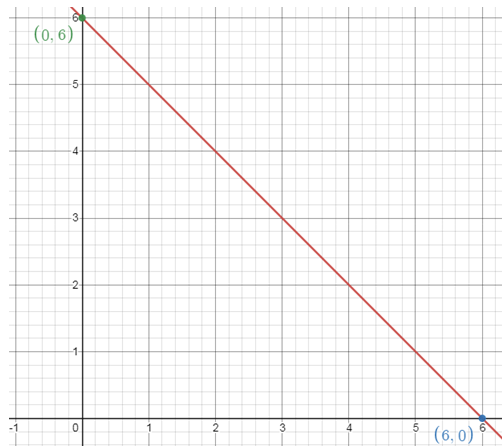
x + y = 6

Solution

Problem 2 :

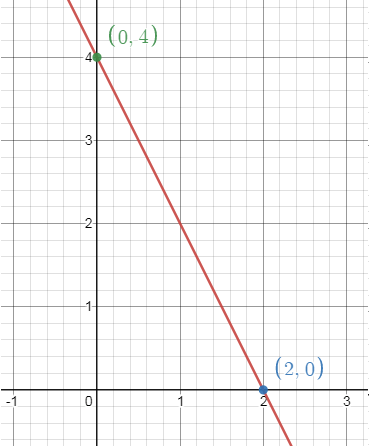
2x + y = 4

Solution

Problem 3 :

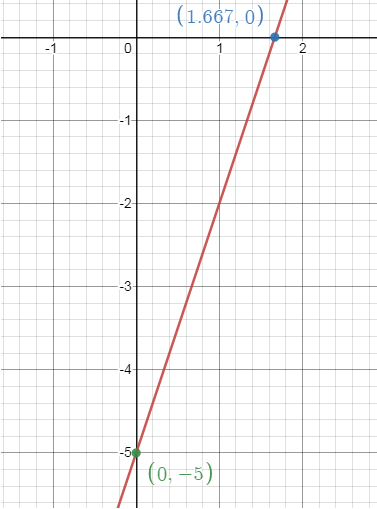
3x - y = 5

Solution

Problem 4 :

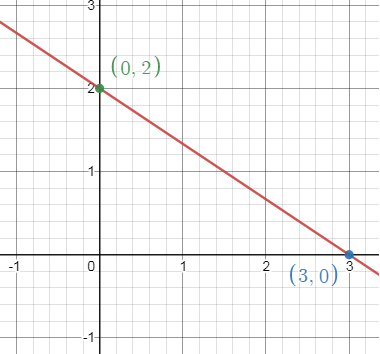
2x + 3y = 6

Solution

Problem 5 :

3x - 4y = 12

Solution

Problem 6 :

x + 3y = -6

Solution

Problem 7 :

2x - 5y = 10

Solution

Problem 8 :

2x + 7y = 14

Solution

Problem 9 :

3x - 4y = 8

Solution

Problem 10 :

You are designing a sticker to advertise your band. A company charges $225 for the first 1000 stickers and $80 for each additional 1000 stickers.

a. Write an equation that represents the total cost (in dollars) of the stickers as a function of the number (in thousands) of stickers ordered.

b. Find the total cost of 9000 stickers.

Solution

Problem 11 :

You pay a processing fee and a daily fee to rent a beach house. The table shows the total cost of renting the beach house for different numbers of days.

a. Can the situation be modeled by a linear equation? Explain.

b. What is the processing fee? the daily fee?

c. You can spend no more than $1200 on the beach house rental. What is the maximum number of days you can rent the beach house?

Solution

Answer Key

1)  

2)

3)

4)

5)

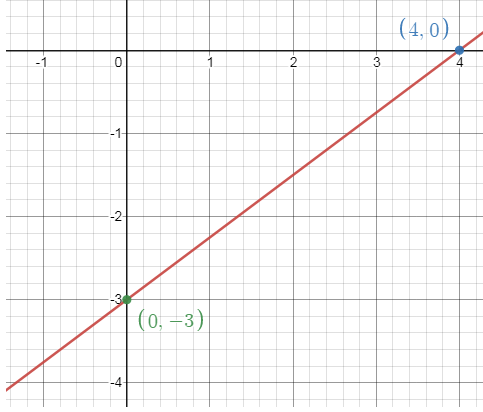
6)

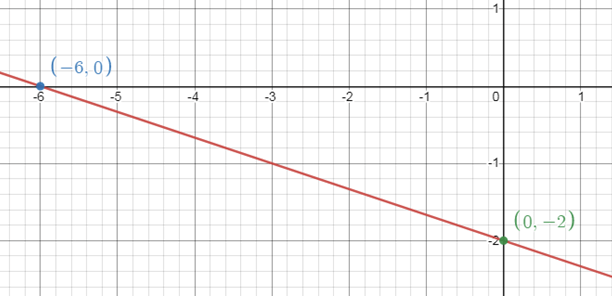
7)

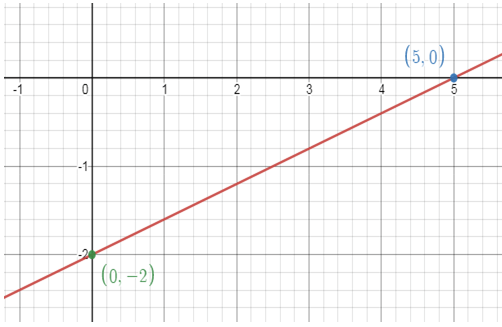
8)

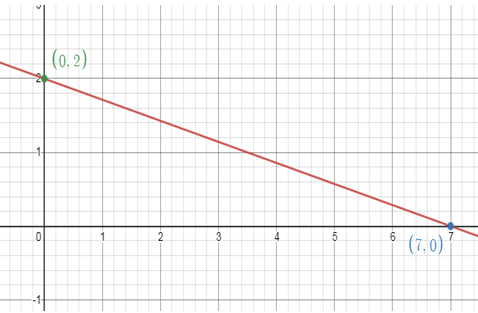
9)  

10) a) y = 2x/25 - 145

b)  the required cost is $575.

11) a) y = 97x + 52

b) Processing fee is $52 and daily fee is $97.

c) Approximately 20 days.

Find the x and y intercept of the line with the given equation.

Problem 1 :

x - y = 4

Solution

Problem 2 :

x + 5y = -15

Solution

Problem 3 :

3x - 4y = -12

Solution

Problem 4 :

2x - y = 10

Solution

Problem 5 :

4x - 5y = 20

Solution

Problem 6 :

-6x + 8y = -36

Solution

Problem 7 :

You are planning an awards banquet for your school. You need to rent tables to seat 180 people. There are two table sizes available. Small tables seat 6 people, and large tables seat 10 people. The equation 6x + 10y = 180 models this situation, where x is the number of small tables and y is the number of large tables.

a. Graph the equation. Interpret the intercepts.

b. Find four possible solutions in the context of the problem.

Solution

Problem 8 :

You are organizing a class trip to an amusement park. The cost to enter the park is $30. The cost to enter with a meal plan is $45. You have a budget of $2700 for the trip. The equation

30x + 45y = 2700

models the total cost for the class to go on the trip, where x is the number of students who do not choose the meal plan and y is the number of students who do choose the meal plan.

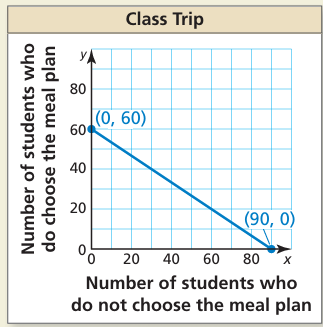
a. Interpret the intercepts of the graph.

b. Describe the domain and range in the context of the problem.

Solution

Find the x and y intercepts and graph each.

Problem 1 :

5y + 4x = 20

Solution

Problem 2 :

-3y + x = 3

Solution

Problem 3 :

-2y + 4x = -8

Solution

Problem 4 :

Identify the slope and y – intercept in y = 4x - 8

Solution

Problem 5 :

The function C(x) = 17.5x − 10 represents the cost (in dollars) of buying x tickets to the orchestra with a $10 coupon.

a. How much does it cost to buy five tickets?

b. How many tickets can you buy with $130?

Solution

Problem 6 :

The function d(t) = 300,000t represents the distance (in kilometers) that light travels in t seconds.

a. How far does light travel in 15 seconds?

b. How long does it take light to travel 12 million kilometers?

Solution

Problem 7 :

An artist rents a booth at an art show for $300. The function f(x) = 50x − 300 represents the artist’s profit, where x is the number of paintings the artist sells. Find the zero of the function. Explain what the zero means in this situation.

Solution