IDENTIFYING X AND Y INTERCEPTS FROM AN EQUATION

Find the x and y intercepts and graph each.

Problem 1 :

5y + 4x = 20

Solution :

Consider the following equation :

5y + 4x = 20

So, x and y intercepts are (5, 0) and (0, 4).

Problem 2 :

-3y + x = 3

Solution :

Consider the following equation :

-3y + x = 3

So, x and y intercepts are (3, 0) and (0, -1).

Problem 3 :

-2y + 4x = -8

Solution :

Consider the following equation :

-2y + 4x = -8

So, x and y intercepts are (-2, 0) and (0, 4).

Problem 4 :

Identify the slope and y – intercept in y = 4x - 8

Solution :

Given, y = 4x - 8

The given equation is in slope intercept form, by comparing the given equation with slope intercept form (y = mx + b), we get

Slope (m) = 4 and y-intercept = -8.

Problem 5 :

The function C(x) = 17.5x − 10 represents the cost (in dollars) of buying x tickets to the orchestra with a $10 coupon.

a. How much does it cost to buy five tickets?

b. How many tickets can you buy with $130?

Solution :

C(x) = 17.5x − 10

a)  x is the number of tickets

Here x = 5

C(5) = 17.5(5) - 10

= 87.5 - 10

= 77.5

b) C(x) = 130

130 = 17.5x − 10

130 + 10 = 17.5 x

17.5x = 140

x = 140/17.5

x = 8

So, we may purchase 8 tickets for $130.

Problem 6 :

The function d(t) = 300,000t represents the distance (in kilometers) that light travels in t seconds.

a. How far does light travel in 15 seconds?

b. How long does it take light to travel 12 million kilometers?

Solution :

d(t) = 300,000t

a)  Number of second t = 15

d(15) = 300000(15)

= 4500000

So, in 15 seconds light travels 4500000.

b)  1200000 = 300,000t

t = 1200000/300000

t = 4

In 4 seconds.

Problem 7 :

An artist rents a booth at an art show for $300. The function f(x) = 50x − 300 represents the artist’s profit, where x is the number of paintings the artist sells. Find the zero of the function. Explain what the zero means in this situation.

Solution :

f(x) = 50x − 300

When f(x) = 0

50x - 300 = 0

50x = 300

x = 300/50

x = 6

The zero of the function is 6. Because the function represents the artist’s profit, the zero of the function represents the number of paintings the artist must sell to recover the cost of renting the booth. So, the artist must sell 6 paintings to recover the cost of renting the booth.

Problem 8 :

The function f (t) = −2t + 25 represents the amount (in gallons) of water remaining in a tub after t seconds. Find the zero of the function. Explain what the zero means in this situation.

You are planning an awards banquet for your school. You need to rent tables to seat 180 people. Tables come in two sizes. Small tables seat 6 people, and large tables seat 10 people. The equation 6x + 10y = 180 models this situation, where x is the number of small tables and y is the number of large tables.

a. Graph the equation. Interpret the intercepts.

b. Find four possible solutions in the context of the problem.

Solution :

You know the equation that models the situation. You are asked to graph the equation, interpret the intercepts, and find four solutions.

Use intercepts to graph the equation. Then use the graph to interpret the intercepts and fi nd other solutions.

Use intercepts to graph the equation. Neither x nor y can be negative, so only graph the equation in the first quadrant.

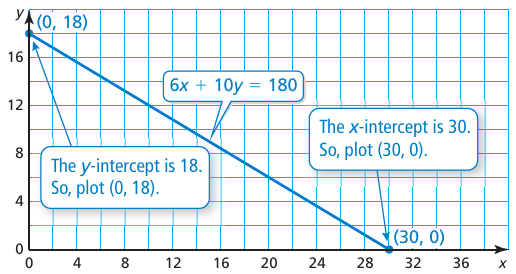
The x-intercept shows that you can rent 30 small tables when you do not rent any large tables. The y-intercept shows that you can rent 18 large tables when you do not rent any small tables.

Only whole-number values of x and y make sense in the context of the problem. Besides the intercepts, it appears that the line passes through the points (10, 12) and (20, 6).

To verify that these points are solutions, check them in the equation, as shown. So, four possible combinations of tables that will seat 180 people are 0 small and 18 large, 10 small and 12 large, 20 small and 6 large, and 30 small and 0 large.

The graph shows that as the number x of small tables increases, the number y of large tables decreases. This makes sense in the context of the problem. So, the graph is reasonable