FIND THE X AND Y INTERCEPTS FROM AN EQUATION OF A LINE

Find the x and y intercept of the line with the given equation.

Problem 1 :

x - y = 4

Solution : 

To find x and y intercept we have to compare given equation with intercept form

(x/a) + (y/b) = 1

x - y = 4

Dividing by 4 on both sides,

x/4 - y/4 = 4/4

(x/4) - (y/4) = 1

x -intercept (a) = 4

y -intercept (b) = - 4

Problem 2 :

x + 5y = -15

Solution :

To find x and y intercept we have to compare given equation with intercept form

(x/a) + (y/b) = 1

x + 5y = -15

Dividing by -15 on both sides,

(x/-15) + (5y/-15) = -15/-15

(x/-15) + (y/-3) = 1

x -intercept (a) = - 15

y -intercept (b) = - 3

Problem 3 :

3x - 4y = -12

Solution :

To find x and y intercept we have to compare given equation with intercept form

(x/a) + (y/b) = 1

3x - 4y = -12

Dividing by -12 on both sides,

(3x/-12) - (4y/-12) = -12/-12

(x/-4) - (y/-3) = 1

x -intercept (a) = - 4

y -intercept (b) = 3

Problem 4 :

2x - y = 10

Solution :

To find x and y intercept we have to compare given equation with intercept form

(x/a) + (y/b) = 1

2x - y = 10

Dividing by 10 on both sides,

(2x/10) - (y/10) = 10/10

(x/5) - (y/10) = 1

x -intercept (a) = 5

y -intercept (b) = - 10

Problem 5 :

4x - 5y = 20

Solution :

To find x and y intercept we have to compare given equation with intercept form

(x/a) + (y/b) = 1

4x - 5y = 20

Dividing by 20 on both sides,

(4x/20) - (5y/20) = 20/20

(x/5) - (y/4) = 1

x -intercept (a) = 5

y -intercept (b) = - 4

Problem 6 :

-6x + 8y = -36

Solution :

To find x and y intercept we have to compare given equation with intercept form

(x/a) + (y/b) = 1

-6x + 8y = -36

Dividing by -36 on both sides,

(-6x/-36) + (8y/-36) = -36/-36

(x/6) + (2y/-9) = 1

x -intercept (a) = 6

y -intercept (b) = - 9/2

Problem 7 :

You are planning an awards banquet for your school. You need to rent tables to seat 180 people. There are two table sizes available. Small tables seat 6 people, and large tables seat 10 people. The equation 6x + 10y = 180 models this situation, where x is the number of small tables and y is the number of large tables.

a. Graph the equation. Interpret the intercepts.

b. Find four possible solutions in the context of the problem.

Solution :

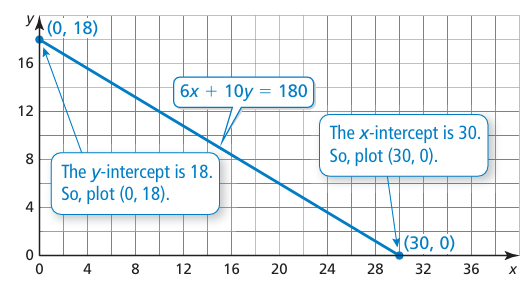
a) The x-intercept shows that you can rent 30 small tables when you do not rent any large tables. The y-intercept shows that you can rent 18 large tables when you do not rent any small tables.

b. Only whole-number values of x and y make sense in the context of the problem. Besides the intercepts, it appears that the line passes through the points (10, 12) and (20, 6).

To verify that these points are solutions, check them in the equation, as shown. So, four possible combinations of tables that will seat 180 people are 0 small and 18 large, 10 small and 12 large, 20 small and 6 large, and 30 small and 0 large. 

Look Back The graph shows that as the number x of small tables increases, the number y of large tables decreases. This makes sense in the context of the problem. So, the graph is reasonable.

Problem 8 :

You are organizing a class trip to an amusement park. The cost to enter the park is $30. The cost to enter with a meal plan is $45. You have a budget of $2700 for the trip. The equation

30x + 45y = 2700

models the total cost for the class to go on the trip, where x is the number of students who do not choose the meal plan and y is the number of students who do choose the meal plan.

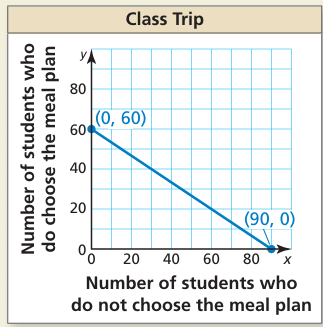
a. Interpret the intercepts of the graph.

b. Describe the domain and range in the context of the problem.

Solution :

30x + 45y = 2700

When x = 0

30(0) + 45y = 2700

45y = 2700

y = 2700/45

y = 60

This means if all 90 students do not choose the meal plan, the budget is fully utilized.

When y = 0

30x + 45(0) = 2700

30x = 2700

x = 2700/30

x = 90

This means if all 60 students choose the meal plan, the budget is fully utilized.

b) 

• The domain is 0 ≤ x ≤ 90
• Range is 0 ≤ y ≤ 60