GRAPH A LINE USING X AND Y INTERCEPTS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Use axes intercepts to draw the graph of:
Problem 1 :
x + y = 6
Solution :
|
x-intercept: Put y = 0 x + y = 6 x + 0 = 6 x = 6 (6, 0) |
y-intercept: Put x = 0 0 + y = 6 y = 6 (0, 6) |
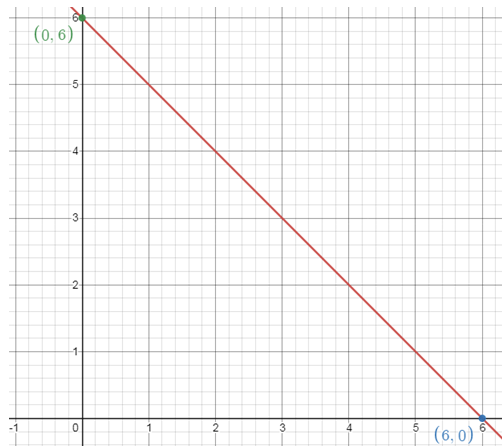
Plot (6, 0)
and (0, 6) by connecting these two points, we will get the line.
Problem 2 :
2x + y = 4
Solution :
|
x-intercept: y = 0 2x + y = 4 2x + 0 = 4 2x = 4 x = 2 (2, 0) |
y-intercept: x = 0 0 + y = 4 y = 4 (0, 4) |
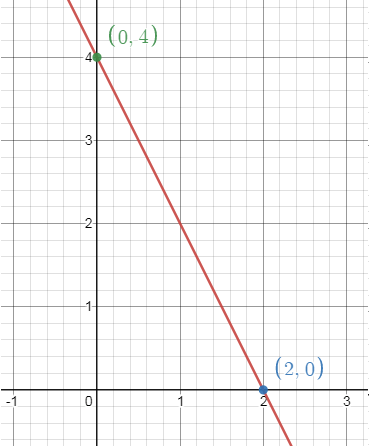
Plot (2, 0)
and (0, 4) by connecting these two points, we will get the line.
Problem 3 :
3x - y = 5
Solution :
|
x-intercept: y = 0 3x - y = 5 3x - 0 = 5 3x = 5 x = 5/3 (5/3, 0) |
y-intercept: x = 0 0 - y = 5 y = -5 (0, -5) |
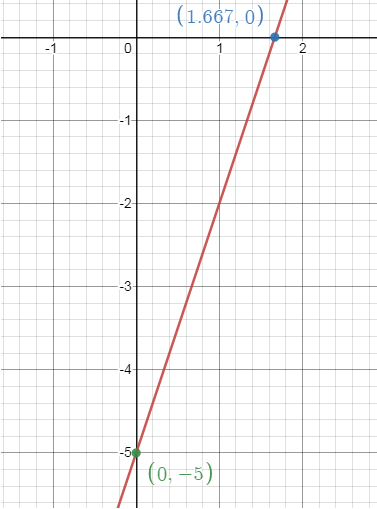
Plot (5/3,
0) and (0, -5) by connecting these two points, we will get the line.
Problem 4 :
2x + 3y = 6
Solution :
|
x-intercept : y = 0 2x + 0 = 6 2x = 6 x = 3 (3, 0) |
y-intercept : x = 0 0 + 3y = 6 3y = 6 y = 2 (0, 2) |
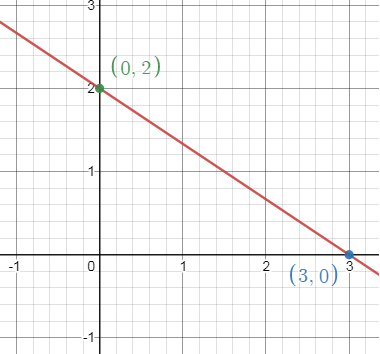
Plot (3, 0)
and (0, 2) by connecting these two points, we will get the line.
Problem 5 :
3x - 4y = 12
Solution :
|
x-intercept : y = 0 3x - 4y = 12 3x - 0 = 12 3x = 12 x = 4 (4, 0) |
y-intercept : x = 0 0 - 4y = 12 -4y = 12 y = -3 (0, -3) |
Plot (4, 0)
and (0, -3) by connecting these two points, we will get the line.
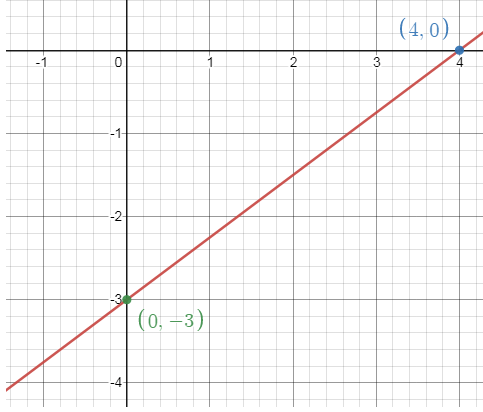
Problem 6 :
x + 3y = -6
Solution :
|
x-intercept : y = 0 x + 0 = -6 x = -6 (-6, 0) |
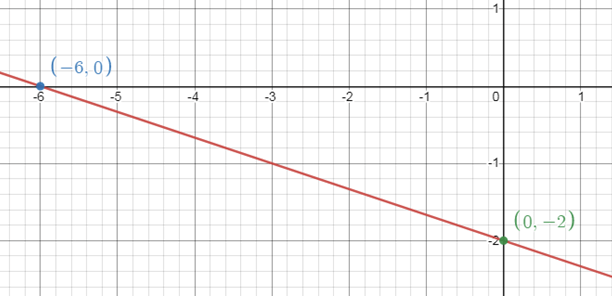
y-intercept : x = 0 0 + 3y = -6 3y = -6 y = -2 (0, -2) |
Plot (-6, 0) and (0, -2) by connecting these two points, we will get the line.
Problem 7 :
2x - 5y = 10
Solution :
|
x-intercept : y = 0 2x - 0 = 10 2x = 10 x = 5 (5, 0) |
y-intercept : x = 0 0 - 5y = 10 -5y = 10 y = -2 (0, -2) |
Plot (5, 0) and (0, -2) by connecting these two points, we will get the line.
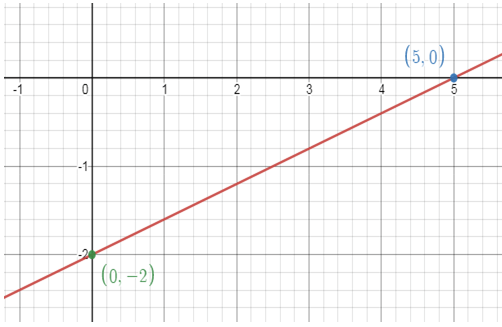
Problem 8 :
2x + 7y = 14
Solution :
|
x-intercept: Put y = 0 2x + 0 = 14 2x = 14 x = 7 (7, 0) |
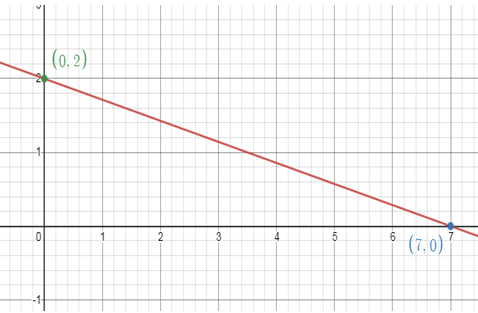
y-intercept : x = 0 0 + 7y = 14 7y = 14 y = 2 (0, 2) |
Plot (7, 0) and (0, 2), by connecting these two points, we will get the line.
Problem 9 :
3x - 4y = 8
Solution :
|
x-intercept: y = 0 3x - 0 = 8 3x = 8 x = 8/3 (8/3, 0) |
y-intercept: x = 0 0 - 4y = 8 -4y = 8 y = -2 (0, -2) |
Plot (8/3, 0) and (0, -2), by connecting these two points, we will get the line.
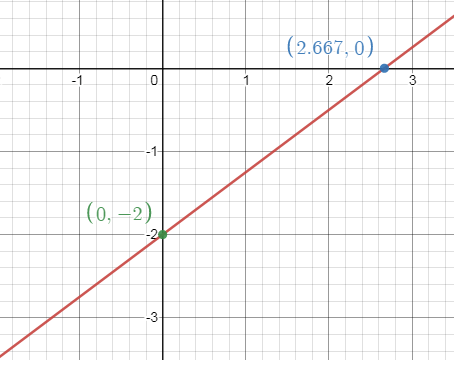
Problem 10 :
You are designing a sticker to advertise your band. A company charges $225 for the first 1000 stickers and $80 for each additional 1000 stickers.
a. Write an equation that represents the total cost (in dollars) of the stickers as a function of the number (in thousands) of stickers ordered.
b. Find the total cost of 9000 stickers.
Solution :
a) Let x be the number of stickers and y be the charge.
(1000, 225) and (2000, 305)
Slope = (y2 - y1) / (x2 - x1)
= (305 - 225) / (2000 - 1000)
= 80/1000
= 2/25
Equation of line :
(y - y1) = m(x - x1)
(y - 225) = (2/25)(x - 1000)
y = 2x/25 - (2/25) ⋅ 1000 + 225
y = 2x/25 - 2 ⋅ 40 + 225
y = 2x/25 - 80 + 225
y = 2x/25 - 145
b) Total cost of 9000 stickers.
y = 2(9000)/25 - 145
= 720 - 145
= 575
So, the required cost is $575.
Problem 11 :
You pay a processing fee and a daily fee to rent a beach house. The table shows the total cost of renting the beach house for different numbers of days.

a. Can the situation be modeled by a linear equation? Explain.
b. What is the processing fee? the daily fee?
c. You can spend no more than $1200 on the beach house rental. What is the maximum number of days you can rent the beach house?
Solution :
Let be the number of days and y be the total cost
(2, 246) and (4, 450)
Slope = (y2 - y1) / (x2 - x1)
= (450 - 246) / (4 - 2)
= 194/2
= 97
Equation of line :
(y - y1) = m(x - x1)
(y - 246) = 97(x - 2)
y = 97x - 194 + 246
y = 97x + 52
b) Processing fee is $52 and daily fee is $97.
c) Amount spend = 2000
2000 = 97x + 52
97x = 2000 - 52
97x = 1948
x = 1948/97
x = 20.08
Approximately 20 days.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling