FINDING THE EQUATION OF A PARABOLA

The graphical form of a quadratic function will be a parabola. The quadratic equation can be converted into different forms.

• Standard form
• Vertex form
• Factored form

Equation of the Parabola Passing Through the Given Points

Problem 1 :

Find a quadratic model for each set of values.

(–1, 1), (1, 1), (3, 9)

Solution :

Let the quadratic model be y = ax² + bx + c

The parabola passes through the given points, so we can apply the points one by one.

It passes through (-1, 1).

1 = a(-1)² + b(-1) + c

1 = a - b + c

a - b + c = 1 -----------(1)

It passes through (1, 1).

1 = a(1)² + b(1) + c

1 = a + b + c

a + b + c = 1 -----------(2)

It passes through (3, 9).

9 = a(3)² + b(3) + c

9 = 9a + 3b + c

9a + 3b + c = 9 -----------(3)

(1) + (2)

a - b + c + a + b + c = 1 + 1

2a + 2c = 2

a + c = 1 ----(4)

Multiply the first equation and subtract (3), we get

3a -

www.cracksat.net

---------------------

Source Url:https://www.cracksat.net/digital/math/question-236-answer-and-explanation.html3b + 3c + 9a + 3b + c = 3+9

12a + 4c = 12 ----(5)

4(4) - (5)

4a + 4c - 12a - 4c = 4 - 12

-8a = -8

a = 1

So, the required equation of parabola is y = x²

Finding Equation in Vertex form

Problem 2 :

Find the quadratic function with the given vertex and point. 

Vertex (2, 0) passing through (1, 3).

Solution :

y = a(x - h)² + k

(h, k) ==>  (2, 0)

y = a(x - 2)² + 0

y = a(x - 2)² ----(1)

The parabola is passing through the point (1, 3).

3 = a(1 - 2)²

3 = a(-1)²

3 = a

Applying the value of a in (1), we get

y = 3(x - 2)²

Equation of parabola from zeroes or x-intercepts

Problem 3 :

Determine the equation of the parabola whose zeroes are 4 and -5 which passes through (2, -42).

Solution :

Zeroes are 4 and -5.

x = 4 and x = -5

Product of factors :

(x - 4)(x + 5)

Writing it as factored form, we get

y = a (x - 4)(x + 5) ------(1)

The parabola passes through the point (2, -42).

-42 = a (2 - 4)(2 + 5)

-42 = a (-2)(7)

a = 42/14

a = 3

By applying the value of a in (1), we get

y = 3(x - 4)(x + 5)

We can convert this into standard form or vertex form. We can check the answer using graphing calculator.

Problem 4 :

Which function is represented by the graph?

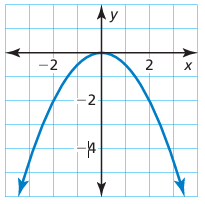
a)  y = (1/2)  x²     b) y = 2x²     c) y = −(1/2)  x²       d)  y = −2x

Solution :

Observing the graph, the parabola opens down. The vertex of the parbola is (0, 0).

y = a(x - h)² + k

Here vertex is at (0, 0).

y = a(x - 0)² + 0

y = ax²

The parabola passes through the point (-2, -2).

-2 = a(-2)²

-2 = 4a

a = -2/4

a = -1/2

By applying the value of a, 

y = (-1/2)x²

So, option c is correct.

Problem 5 :

In the xy-plane above y = a(x - h)² has one x-intercept at (4, 0). If the y-intercept of the parabola is 9, what is the value of a ?

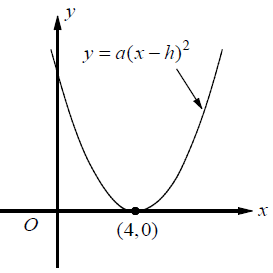
Solution :

y = a(x - h)²

By applying the point (4, 0), we get

y = a(x - 4)²

The y-intercept of the parabola is 9. Then applying the point (0, 9), we get

9 = a(0 - 4)²

9 = 16a

a = 9/16

So, the value of a is 9/16.

Problem 6 :

Tell whether the function has minimum value or maximum value, then find the value.

i)  5x² - 20x + 3

ii)  -3x² + 12x - 7

Solution :

i)  5x² - 20x + 3

y = 5x² - 20x + 3

Factroing 5, 

y = 5[x² - 4x] + 3

y = 5[(x - 2)² - 4] + 3

y = 5(x - 2)² - 20 + 3

y = 5(x - 2)² - 17

• The parabola opens up.
• It has minimum value
• Minimum is at (2, -17).

ii)  -3x² + 12x - 7

Factroing -3, 

y = -3[x² - 4x] - 7

y = -3[(x - 2)² - 4] - 7

y = -3(x - 2)² + 12 - 7

y = -3(x - 2)² + 5

• The parabola opens up.
• It has maximum value
• Maximum is at (2, 5).

Related pages

• Converting from standard form to vertex form
• Converting from vertex form to standard form
• Converting from standard form to factored form