CONVERTING FROM STANDARD INTO VERTEX FORM
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
To convert standard form to vertex form, we may follow the different ways.
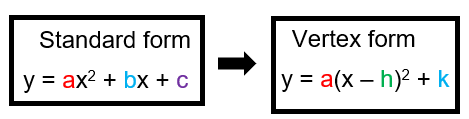
Completing the square method
From the standard form of the equation, y = ax2 + bx + c
(i) Take the coefficient of x2, from all the terms if there is.
(ii) Write the coefficient of x as a multiple of 2.
(iii) Get any one of the algebraic identities (a+b)2 or (a-b)2
Example :
Convert the following quadratics from standard form to vertex form
y = 2x2 – 4x + 8
Solution :
y = 2x2 – 4x + 8
Factor 2.
y = 2(x2 – 2x + 4)
Write the coefficient of x as a multiple of 2.
y = 2(x2 – 2⋅x⋅1 + 12 - 12 + 4)
Here x2 – 2⋅x⋅1 + 12 matches with a2 – 2⋅a⋅b + b2 = (a - b)2
y = 2[(x - 1)2 - 1 + 4]
y = 2[(x - 1)2 + 3]
Distributing 2, we get
y = 2(x - 1)2 + 6
Using short cut
From the standard form of the equation, y = ax2 + bx + c
(i) Take the coefficient of x2, from all the terms if there is.
(ii) Take half of the coefficient of x and write it as (x - a)2 or (x + a)2. Here a is half the coefficient of x.
Example :
Convert y = x2 - 4x + 3 into factored form.
Solution :
y = x2 - 4x + 3
Coefficient of x2 is 1, so dont have to factor anything.
Half of the coefficient of x is 2.
y = (x - 2)2 - 22 + 3
y = (x - 2)2 - 4 + 3
y = (x - 2)2 - 1
More Examples
Complete the square to convert the standard form quadratic function into vertex form. Then
find the vertex.
Example 1 :
f(x) = x2 + 4x - 14
Solution :
Coefficient of x2 is 1. So, don't have to factorize.
Write the coefficient of x as multiple of 2.
f(x) = x2 + 2 ⋅ x ⋅ 2 + 22 - 22 - 14
f(x) = (x+2)2 - 4 - 14
f(x) = (x+2)2 - 18
Example 2 :
f(x) = 2x2 + 9x
Solution :
Coefficient of x2 is 2.
Write the coefficient of x as multiple of 2.
Example 3 :
f(x) = 5x2 - 4x + 1
Solution :
Coefficient of x2 is 5. So, we have to factorize 5.
Example 4 :
f(x) = x2 - 16x + 70
Solution :
Coefficient of x2 is 1. So, don't have to factorize.
Write the coefficient of x as multiple of 2.
f(x) = x2 - 2 ⋅ x ⋅ 8 + 82 - 82 + 70
f(x) = (x - 8)2 - 64 + 70
f(x) = (x - 8)2 + 6
Example 5 :
f(x) = -3x2 + 48x - 187
Solution :
Coefficient of x2 is -3. So, factorize -3.
f(x) = -3[x2 - 16x] - 187
Write the coefficient of x as multiple of 2.
f(x) = -3[x2 - 2 ⋅ x ⋅ 8 + 82- 82] - 187
f(x) = -3[(x - 8)2- 64] - 187
f(x) = -3(x - 8)2+ 192 - 187
f(x) = -3(x - 8)2+ 5
Related Pages
- Converting from standard into vertex form
- Converting from vertex form to standard form
- Examples on converting from standard form to factored form
- Converting from standard form to factored form worksheet
- Converting from Standard form to vertex form
- Converting from standard form to vertex form worksheet
- Converting from standard form to factored form
- Converting between different forms of quadratic functions worksheet
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling